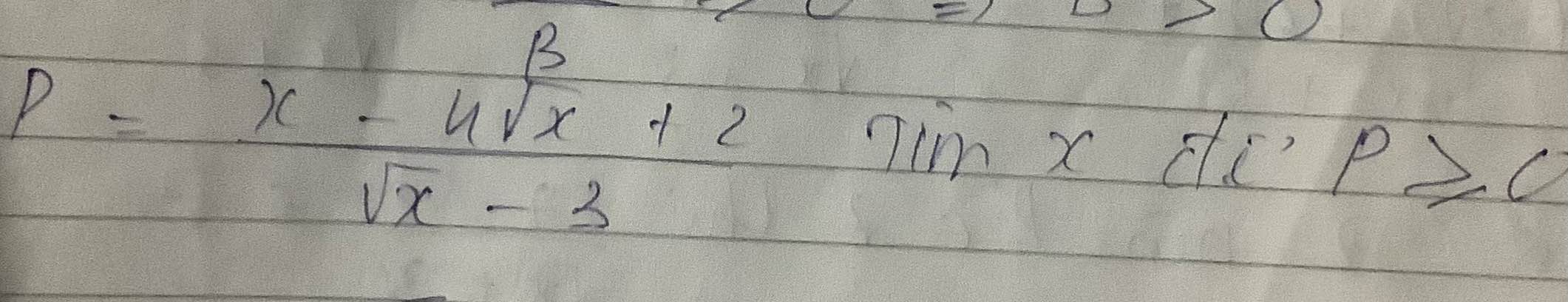\(P>=0\)
=>\(\dfrac{x-4\sqrt{x}+2}{\sqrt{x}-3}>=0\)
=>\(\dfrac{x-4\sqrt{x}+4-2}{\sqrt{x}-3}>=0\)
=>\(\dfrac{\left(\sqrt{x}-2\right)^2-2}{\sqrt{x}-3}>=0\)
TH1: \(\left\{{}\begin{matrix}\left(\sqrt{x}-2\right)^2-2< =0\\\sqrt{x}-3< 0\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}\left(\sqrt{x}-2\right)^2< =2\\\sqrt{x}< 3\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}-\sqrt{2}< =\sqrt{x}-2< =\sqrt{2}\\0< =x< 9\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}2-\sqrt{2}< =\sqrt{x}< =2+\sqrt{2}\\0< =x< 9\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}6-4\sqrt{2}< =x< =6+4\sqrt{2}\\0< =x< 9\end{matrix}\right.\Leftrightarrow6-4\sqrt{2}< =x< 9\)
TH2: \(\)\(\left\{{}\begin{matrix}\left(\sqrt{x}-2\right)^2-2>=0\\\sqrt{x}-3>0\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}\left(\sqrt{x}-2\right)^2>=2\\\sqrt{x}>3\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}\left[{}\begin{matrix}\sqrt{x}-2>=\sqrt{2}\\\sqrt{x}-2< =-\sqrt{2}\end{matrix}\right.\\x>9\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}\left\{{}\begin{matrix}\sqrt{x}>=2+\sqrt{2}\\x>9\end{matrix}\right.\\\left\{{}\begin{matrix}\sqrt{x}< =2-\sqrt{2}\\x>9\end{matrix}\right.\end{matrix}\right.\)
=>\(\left[{}\begin{matrix}\left\{{}\begin{matrix}x>=\left(2+\sqrt{2}\right)^2=6+4\sqrt{2}\\x>9\end{matrix}\right.\\\left\{{}\begin{matrix}x< =\left(2-\sqrt{2}\right)^2=6-4\sqrt{2}\\x>9\end{matrix}\right.\left(loại\right)\end{matrix}\right.\)
=>x>9