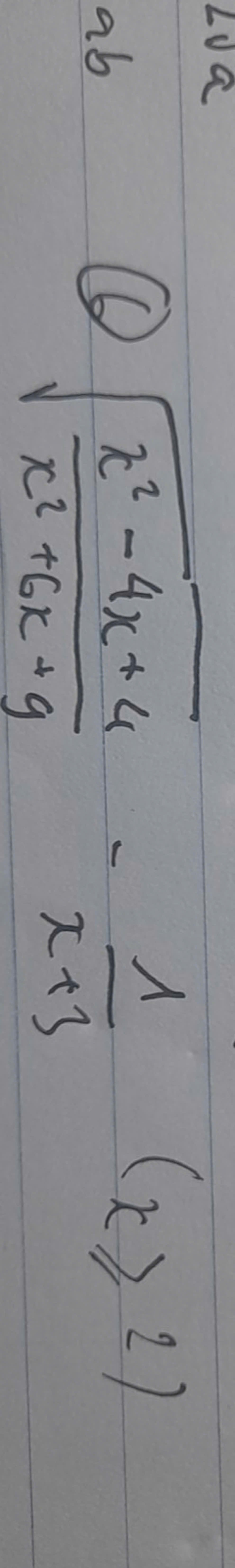\(\sqrt{\dfrac{x^2-4x+4}{x^2+6x+9}}-\dfrac{1}{x+3}\left(x\ge2\right)\\ =\sqrt{\dfrac{\left(x-2\right)^2}{\left(x+3\right)^2}}-\dfrac{1}{x+3}\\ =\dfrac{\left|x-2\right|}{\left|x+3\right|}-\dfrac{1}{x+3}\\ =\dfrac{x-2}{x+3}-\dfrac{1}{x+3}=\dfrac{x-3}{x+3}\)
Giải thích: Vì: x>=2 => x-2>=0 => |x-2|=x-2
và x>=2 => x+3>=5 => |x+3|=x+3
\(\sqrt{\dfrac{x^2-4x+4}{x^2+6x+9}}-\dfrac{1}{x+3}=\sqrt{\dfrac{\left(x-2\right)^2}{\left(x+3\right)^2}}-\dfrac{1}{x+3}\)
\(=\dfrac{\left|x-2\right|}{\left|x+3\right|}-\dfrac{1}{x+3}=\dfrac{x-2}{x+3}-\dfrac{1}{x+3}\)
\(=\dfrac{x-3}{x+3}\)