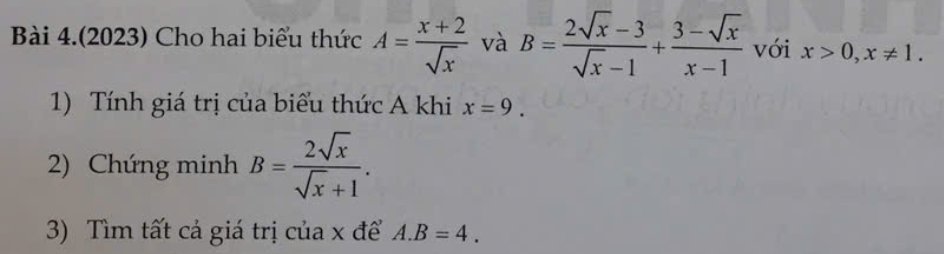1: Thay x=9 vào A, ta được:
\(A=\dfrac{9+2}{3}=\dfrac{11}{3}\)
2: \(B=\dfrac{2\sqrt{x}-3}{\sqrt{x}-1}+\dfrac{3-\sqrt{x}}{x-1}\)
\(=\dfrac{2\sqrt{x}-3}{\sqrt{x}-1}+\dfrac{3-\sqrt{x}}{\left(\sqrt{x}-1\right)\left(\sqrt{x}+1\right)}\)
\(=\dfrac{\left(2\sqrt{x}-3\right)\left(\sqrt{x}+1\right)+3-\sqrt{x}}{\left(\sqrt{x}-1\right)\left(\sqrt{x}+1\right)}\)
\(=\dfrac{2x+2\sqrt{x}-3\sqrt{x}-3+3-\sqrt{x}}{\left(\sqrt{x}-1\right)\left(\sqrt{x}+1\right)}=\dfrac{2x-2\sqrt{x}}{\left(\sqrt{x}-1\right)\left(\sqrt{x}+1\right)}=\dfrac{2\sqrt{x}}{\sqrt{x}+1}\)
3: AB=4
=>\(\dfrac{2\sqrt{x}}{\sqrt{x}+1}\cdot\dfrac{x+2}{\sqrt{x}}=4\)
=>\(\dfrac{x+2}{\sqrt{x}+1}=2\)
=>\(x+2=2\sqrt{x}+2\)
=>\(x-2\sqrt{x}=0\)
=>\(\sqrt{x}\left(\sqrt{x}-2\right)=0\)
mà x>0
nên \(\sqrt{x}-2=0\)
=>x=4(nhận)