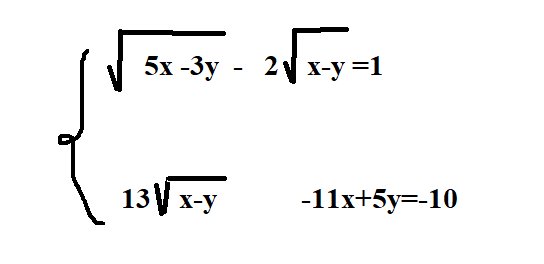Đặt \(\left\{{}\begin{matrix}\sqrt{5x-3y}=a\ge0\\\sqrt{x-y}=b\ge0\end{matrix}\right.\)
\(\Rightarrow11x-5y=3a^2-4b^2\)
Hệ trở thành:
\(\left\{{}\begin{matrix}a-2b=1\\13b-\left(3a^2-4b^2\right)=-10\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}a=2b+1\\13b-3a^2+4b^2+10=0\end{matrix}\right.\)
\(\Rightarrow13b-3\left(2b+1\right)^2+4b^2+10=0\)
\(\Leftrightarrow-8b^2+b+7=0\Rightarrow\left[{}\begin{matrix}b=1\Rightarrow a=3\\b=-\dfrac{7}{8}< 0\left(loại\right)\end{matrix}\right.\)
\(\Rightarrow\left\{{}\begin{matrix}\sqrt{x-y}=1\\\sqrt{5x-3y}=3\end{matrix}\right.\) \(\Leftrightarrow\left\{{}\begin{matrix}x-y=1\\5x-3y=9\end{matrix}\right.\)
\(\Rightarrow\left\{{}\begin{matrix}x=3\\y=2\end{matrix}\right.\)