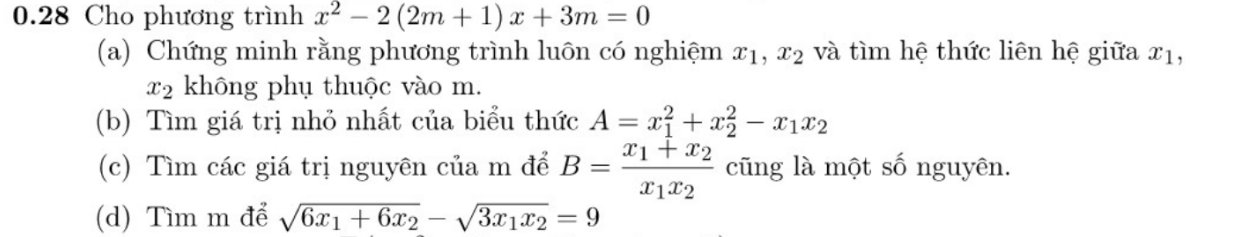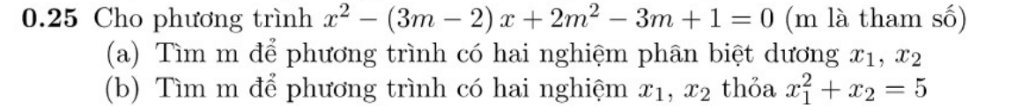Bài 28:
\(x^2-2\left(2m+1\right)x+3m=0\left(1\right)\)
a) Để (1) có nghiệm khi và chỉ khi
\(\Delta'=\left(2m+1\right)^2-3m\ge0\)
\(\Leftrightarrow4m^2+4m+1-3m\ge0\)
\(\Leftrightarrow4m^2+m+1\ge0\)
mà \(\Delta_m=1-4=-3< 0\) và \(4>0\)
\(\Rightarrow4m^2+m+1\ge0,\forall m\in R\)
\(\Rightarrow\) (1) luôn có nghiệm \(x_1;x_2\) \(\left(đpcm\right)\)
Theo định lý Vi ét :
\(\left\{{}\begin{matrix}x_1+x_2=2\left(m+1\right)\\x_1.x_2=3m\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}x_1+x_2=2m+2\\x_1.x_2=3m\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}3\left(x_1+x_2\right)=3\left(2m+2\right)=6m+6\left(a\right)\\2x_1.x_2=6m\left(b\right)\end{matrix}\right.\)
\(\left(a\right)-\left(b\right)\Rightarrow3\left(x_1+x_2\right)-2x_1.x_2=6\) là hệ thức không phụ thuộc vào m
b) \(A=x_1^2+x^2_2-x_1.x_2\)
\(\Leftrightarrow A=\left(x_1+x_2\right)^2-3x_1.x_2\)
\(\Leftrightarrow A=4\left(m+1\right)^2-9m=4m^2+8m+4-9m=4m^2-m+4\)
\(\Leftrightarrow A=4\left(m^2-\dfrac{1}{4}m+\dfrac{1}{64}\right)-\dfrac{1}{16}+4\)
\(\Leftrightarrow A=4\left(m-\dfrac{1}{8}\right)^2+\dfrac{63}{16}\ge\dfrac{63}{16},\forall m\in R\)
Vậy \(GTNN\left(A\right)=\dfrac{63}{16}\left(m=\dfrac{1}{8}\right)\)
Bài 25 :
\(x^2-\left(3m-2\right)x+2m^2-3m+1=0\left(1\right)\)
Để (1) có 2 nghiệm phân biệt dương \(x_1;x_2\)
\(\Leftrightarrow\left\{{}\begin{matrix}\Delta=\left(3m-2\right)^2-4\left(2m^2-3m+1\right)>0\\S=3m-2>0\\P=2m^2-3m+1>0\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}9m^2-12m+4-8m^2+12m-4>0\\m>\dfrac{2}{3}\\P=2\left(m-1\right)\left(m-\dfrac{1}{2}\right)>0\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}m^2>0\\m>\dfrac{2}{3}\\m< \dfrac{1}{2}\cup m>1\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}m\ne0\\m>\dfrac{2}{3}\\m< \dfrac{1}{2}\cup m>1\end{matrix}\right.\)
\(\Leftrightarrow m>1\) (thỏa mãn đề bài)
Ta có :
\(x^2_1+x^2_2=5\)
\(\Leftrightarrow\left(x_1+x_2\right)^2-2x_1x_2=5\)\(\)
\(\Leftrightarrow\left(3m-2\right)^2-2\left(2m^2-3m+1\right)=5\)
\(\Leftrightarrow9m^2-12m+4-4m^2+6m-2-5=0\)
\(\Leftrightarrow5m^2-6m-3=0\)
\(\Leftrightarrow\left[{}\begin{matrix}m=\dfrac{3+2\sqrt{6}}{5}\\m=\dfrac{3-2\sqrt{6}}{5}\left(ktm.m>1\right)\end{matrix}\right.\)
Vậy \(m=\dfrac{3+2\sqrt{6}}{5}\) thỏa mãn yêu cầu đề bài