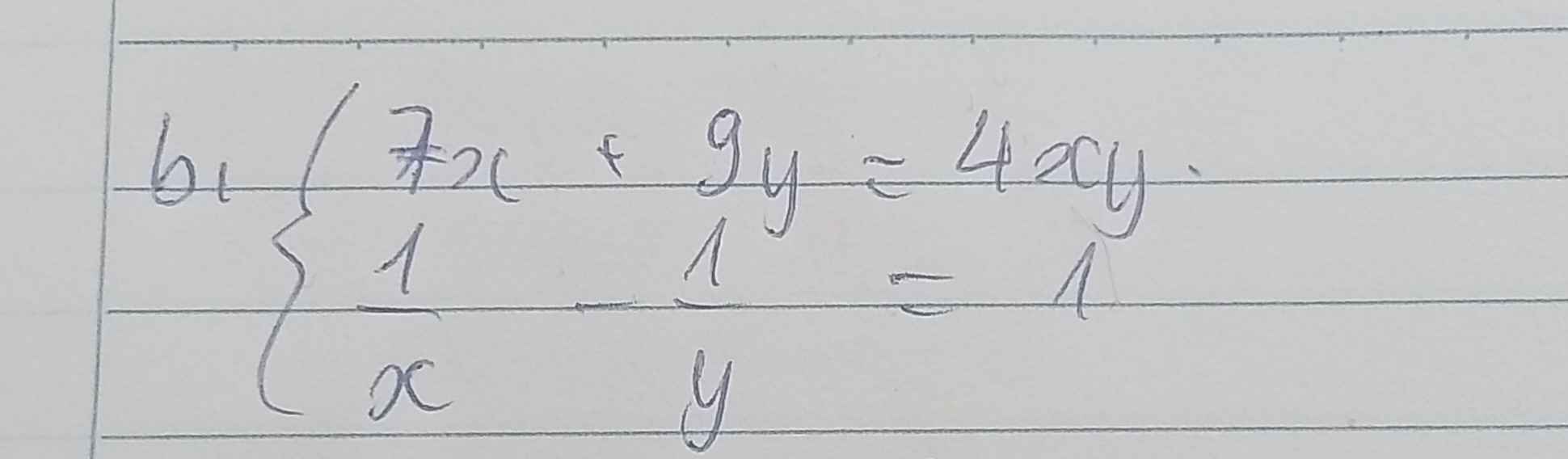ĐKXĐ: \(x;y\ne0\)
\(\Rightarrow\left\{{}\begin{matrix}\dfrac{7x+9y}{xy}=4\\\dfrac{1}{x}-\dfrac{1}{y}=1\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}\dfrac{9}{x}+\dfrac{7}{y}=4\\\dfrac{1}{x}-\dfrac{1}{y}=1\end{matrix}\right.\)
Đặt \(\left\{{}\begin{matrix}\dfrac{1}{x}=u\\\dfrac{1}{y}=v\end{matrix}\right.\) ta được:
\(\left\{{}\begin{matrix}9u+7v=4\\u-v=1\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}u=\dfrac{11}{16}\\v=-\dfrac{5}{16}\end{matrix}\right.\) \(\Rightarrow\left\{{}\begin{matrix}\dfrac{1}{x}=\dfrac{11}{16}\\\dfrac{1}{y}=-\dfrac{5}{16}\end{matrix}\right.\)
\(\Rightarrow\left\{{}\begin{matrix}x=\dfrac{16}{11}\\y=-\dfrac{16}{5}\end{matrix}\right.\)
b,7x + 9y =4xy
\(\dfrac{1}{x}\)-\(\dfrac{1}{y}\) =1
ĐK :
⇒\(\dfrac{7x+9y}{xy}\)=4
\(\dfrac{1}{x}\)-\(\dfrac{1}{y}\)=1
⇒\(\dfrac{7}{y}\)+\(\dfrac{9}{x}\)=4
\(\dfrac{1}{x}\)-\(\dfrac{1}{y}\)=1
Đặt \(\dfrac{1}{x}\)=a;\(\dfrac{1}{y}\)=b khi đó hệ phương trình trở thành:
9a+7b=4
a-b=1
⇔9a+7b=4
7a-7b=7
⇔16a=11
a-b=1
⇔a=\(\dfrac{11}{16}\)
\(\dfrac{11}{16}\)-b=1
⇔ a=\(\dfrac{11}{16}\)
b = - \(\dfrac{5}{16}\)
⇒ \(\dfrac{1}{x}\)=\(\dfrac{11}{16}\)
\(\dfrac{1}{y}\)= - \(\dfrac{5}{16}\)
⇒ x= \(\dfrac{16}{11}\)(thỏa mãn)
y= - \(\dfrac{16}{5}\)(thỏa mãn)
Vậy hệ phương trình có nghiệm duy nhất( x;y ) =(\(\dfrac{16}{11}\);- \(\dfrac{16}{5}\))