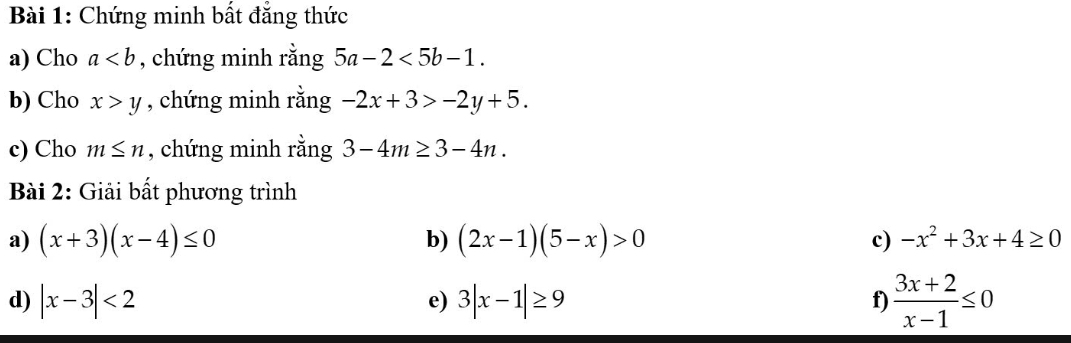Bài 1:
a: a<b
=>5a<5b
=>5a-2<5b-2
mà 5b-2<5b-1
nên 5a-2<5b-1
b: x>y
=>-2x<-2y
=>-2x+3<-2y+3
mà -2y+3<-2y+5
nên -2x+3<-2y+5
c: m<=n
=>-4m>=-4n
=>-4m+3>=-4n+3
Bài 2:
a: (x+3)(x-4)<=0
TH1: \(\left\{{}\begin{matrix}x+3>=0\\x-4< =0\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}x>=-3\\x< =4\end{matrix}\right.\)
=>-3<=x<=4
TH2: \(\left\{{}\begin{matrix}x+3< =0\\x-4>=0\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}x< =-3\\x>=4\end{matrix}\right.\)
=>LOại
b: (2x-1)(5-x)>0
=>(2x-1)(x-5)<0
TH1: \(\left\{{}\begin{matrix}2x-1>0\\x-5< 0\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}x>\dfrac{1}{2}\\x< 5\end{matrix}\right.\)
=>\(\dfrac{1}{2}< x< 5\)
TH2: \(\left\{{}\begin{matrix}2x-1< 0\\x-5>0\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}x< \dfrac{1}{2}\\x>5\end{matrix}\right.\)
=>Loại
c: \(-x^2+3x+4>=0\)
=>\(x^2-3x-4< =0\)
=>(x-4)(x+1)<=0
TH1: \(\left\{{}\begin{matrix}x-4>=0\\x+1< =0\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}x>=4\\x< =-1\end{matrix}\right.\)
=>Loại
TH2: \(\left\{{}\begin{matrix}x-4< =0\\x+1>=0\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}x< =4\\x>=-1\end{matrix}\right.\)
=>-1<=x<=4
d:
|x-3|<2
=>-2<x-3<2
=>-2+3<x<2+3
=>1<x<5
e: 3|x-1|>=9
=>|x-1|>=3
=>\(\left[{}\begin{matrix}x-1>=3\\x-1< =-3\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}x>=4\\x< =-2\end{matrix}\right.\)
f: ĐKXĐ: \(x\ne1\)
\(\dfrac{3x+2}{x-1}< =0\)
TH1: \(\left\{{}\begin{matrix}3x+2>=0\\x-1< 0\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}x>=-\dfrac{2}{3}\\x< 1\end{matrix}\right.\)
=>\(-\dfrac{2}{3}< =x< 1\)
TH2: \(\left\{{}\begin{matrix}3x+2< =0\\x-1>0\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}x< =-\dfrac{2}{3}\\x>1\end{matrix}\right.\)
=>\(x\in\varnothing\)