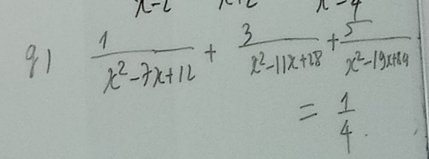\(\dfrac{1}{x^2-7x+12}+\dfrac{3}{x^2-11x+28}+\dfrac{5}{x^2-19x+84}=\dfrac{1}{4}\) (ĐK:\(x\ne\left\{3;4;7;12\right\}\))
\(\Leftrightarrow\dfrac{1}{\left(x-3\right)\left(x-4\right)}+\dfrac{3}{\left(x-4\right)\left(x-7\right)}+\dfrac{5}{\left(x-7\right)\left(x-12\right)}=\dfrac{1}{4}\)
\(\Leftrightarrow\dfrac{1}{x-4}-\dfrac{1}{x-3}+\dfrac{1}{x-7}-\dfrac{1}{x-4}+\dfrac{1}{x-12}-\dfrac{1}{x-7}=\dfrac{1}{4}\)
\(\Leftrightarrow\dfrac{1}{x-12}-\dfrac{1}{x-3}=\dfrac{1}{4}\)
\(\Leftrightarrow\dfrac{x-3-x+12}{\left(x-3\right)\left(x-12\right)}=\dfrac{1}{4}\)
\(\Leftrightarrow\dfrac{9}{x^2-15x+36}=\dfrac{1}{4}\)
\(\Leftrightarrow x^2-15x+36=36\)
\(\Leftrightarrow x^2-15x=0\)
\(\Leftrightarrow x\left(x-15\right)=0\)
\(\Leftrightarrow\left[{}\begin{matrix}x=0\\x=15\end{matrix}\right.\) (T/m)