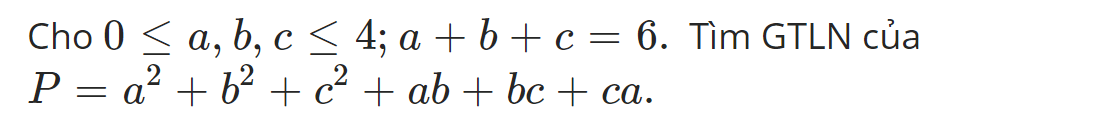Do \(a+b+c=6\) và \(a,b,c\ge0\) nên tồn tại 1 trong 3 số a,b,c không lớn hơn 2. Không giảm tổng quát, giả sử \(c\ge2\). Khi đó \(a+b\le4\). Để ý do \(c\le4\) nên \(a+b\ge2\)
\(\Rightarrow\left(a+b-2\right)\left(a+b-4\right)\le0\Leftrightarrow\left(a+b\right)^2\le6\left(a+b\right)-8\)
Ta có: \(P=a^2+b^2+c^2+ab+bc+ca\)
\(=\dfrac{1}{2}\left(a^2+b^2+c^2\right)+\dfrac{1}{2}\left(a+b+c\right)^2\)
\(=\dfrac{1}{2}\left[a^2+b^2+\left(6-a-b\right)^2\right]+18\)
\(=a^2+b^2+ab-6\left(a+b\right)+36\)
\(=\left(a+b\right)^2-ab-6\left(a+b\right)+36\)
\(\le\left(a+b\right)^2-6\left(a+b\right)+8+28\le28\)
Đẳng thức xảy ra khi \(\left[{}\begin{matrix}a+b=2\\a+b=4\end{matrix}\right.;ab=0\) và các hoán vị , hay \(\left(a,b,c\right)=\left(0,2,4\right)\) và các hoán vị.
Vậy GTLN của P là 28.