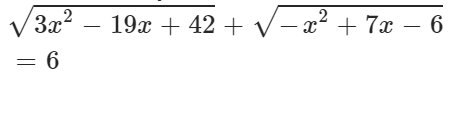:)
\(\sqrt{3x^2-19x+42}+\sqrt{-x^2+7x-6}=6\)
\(\Rightarrow\sqrt{3x^2-19x+42}=6-\sqrt{-x^2+7x-6}\)
\(\Rightarrow3x^2-19x+42=36-12\sqrt{-x^2+7x-6}-x^2+7x-6\)
\(\Rightarrow12\sqrt{-x^2+7x-6}=-4x^2+26x-12\)
\(\Rightarrow6\sqrt{-x^2+7x-6}=-2x^2+13x-6\)
\(\Rightarrow36\left(-x^2+7x-6\right)=\left(-2x^2+13x-6\right)^2\)
\(\Rightarrow4x^4-52x^3+193x^2-156x+36=-36x^2+252x-216\)
\(\Rightarrow4x^4-52x^3+229x^2-408x+252=0\)
\(\Rightarrow\left(2x-7\right)\left(x-6\right)\left(x-2\right)\left(2x-3\right)=0\)
\(\Rightarrow\left[{}\begin{matrix}x=\dfrac{7}{2}\\x=6\\x=2\\x=\dfrac{3}{2}\end{matrix}\right.\)
Thử lại, phương trình đã cho có 4 nghiệm phân biệt là 7/2 ; 6 ; 2 và 3/2.