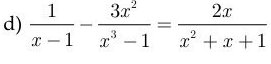ĐKXĐ: \(x\ne1\)
\(\dfrac{1}{x-1}-\dfrac{3x^2}{x^3-1}=\dfrac{2x}{x^2+x+1}\\ \Leftrightarrow\dfrac{x^2+x+1}{\left(x-1\right)\left(x^2+x+1\right)}-\dfrac{3x^2}{\left(x-1\right)\left(x^2+x+1\right)}=\dfrac{2x\left(x-1\right)}{\left(x-1\right)\left(x^2+x+1\right)}\\ \Rightarrow x^2+x+1-3x^2=2x^2-2x\\ \Leftrightarrow-2x^2+x+1=2x^2-2x\\ \Leftrightarrow4x^2-3x-1=0\\ \Leftrightarrow4x^2-4x+x-1=0\\ \Leftrightarrow4x\left(x-1\right)+\left(x-1\right)=0\\ \Leftrightarrow\left(x-1\right)\left(4x+1\right)=0\\ \Leftrightarrow\left[{}\begin{matrix}x-1=0\\4x+1=0\end{matrix}\right.\\ \Leftrightarrow\left[{}\begin{matrix}x=1\\x=-\dfrac{1}{4}\end{matrix}\right.\)
#$\mathtt{Toru}$