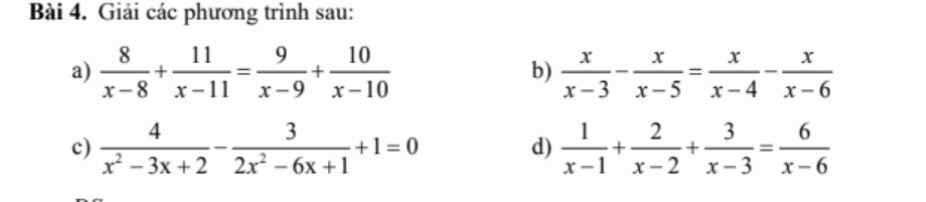Bài 4:
a)
\(\dfrac{8}{x-8}+\dfrac{11}{x-11}=\dfrac{9}{x-9}+\dfrac{10}{x-10}\left(x\ne8;9;10;11\right)\\ \Leftrightarrow\left(\dfrac{8}{x-8}+1\right)+\left(\dfrac{11}{x-11}+1\right)=\left(\dfrac{9}{x-9}+1\right)+\left(\dfrac{10}{x-10}+1\right)\\ \Leftrightarrow\dfrac{x}{x-8}+\dfrac{x}{x-11}=\dfrac{x}{x-9}+\dfrac{x}{x-10}\\ \Leftrightarrow x\left(\dfrac{1}{x-8}+\dfrac{1}{x-11}-\dfrac{1}{x-9}-\dfrac{1}{x-10}\right)=0\\ TH1:x=0\left(tm\right)\)
\(TH2:\dfrac{1}{x-8}+\dfrac{1}{x-11}-\dfrac{1}{x-9}-\dfrac{1}{x-10}=0\\ \Leftrightarrow\dfrac{1}{x-8}+\dfrac{1}{x-11}=\dfrac{1}{x-9}+\dfrac{1}{x-10}\\ \Leftrightarrow\dfrac{x-11+x-8}{\left(x-8\right)\left(x-11\right)}=\dfrac{x-10+x-9}{\left(x-9\right)\left(x-10\right)}\\ \Leftrightarrow\dfrac{2x-19}{\left(x-8\right)\left(x-11\right)}-\dfrac{2x-19}{\left(x-9\right)\left(x-10\right)}=0\\ \Leftrightarrow\left(2x-19\right)\left[\dfrac{1}{\left(x-8\right)\left(x-11\right)}-\dfrac{1}{\left(x-9\right)\left(x-10\right)}\right]=0\\ \Leftrightarrow2x-19=0\Leftrightarrow x=\dfrac{19}{2}\)
Vì: \(\dfrac{1}{\left(x-8\right)\left(x-11\right)}-\dfrac{1}{\left(x-9\right)\left(x-10\right)}\ne0\)