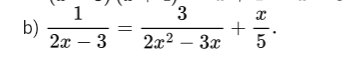\(\dfrac{1}{2x-3}=\dfrac{3}{2x^2-3x}+\dfrac{x}{5}\) (1)
ĐK: \(\left\{{}\begin{matrix}2x-3\ne0\\2x^2-3x\ne0\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x\ne\dfrac{3}{2}\\x\ne0\end{matrix}\right.\)
(1) \(\Leftrightarrow\dfrac{1}{2x-3}=\dfrac{3}{x\left(2x-3\right)}+\dfrac{x}{5}\)
\(\Leftrightarrow\dfrac{5x}{5x\left(2x-3\right)}=\dfrac{15}{5x\left(2x-3\right)}+\dfrac{x^2\left(2x-3\right)}{5x\left(2x-3\right)}\)
\(\Leftrightarrow5x=15+x^2\left(2x-3\right)\)
\(\Leftrightarrow5x=15+2x^3-3x^2\)
\(\Leftrightarrow2x^3-3x^2-5x+15=0\)
\(\Leftrightarrow x\approx-1,898\) (sử dụng máy tính)
Vậy: ...
Đúng 3
Bình luận (0)
