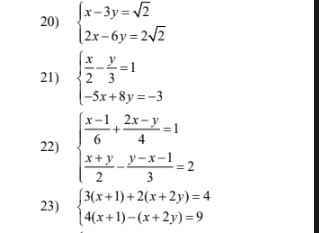20: Vì \(\dfrac{1}{2}=\dfrac{-3}{-6}=\dfrac{\sqrt{2}}{2\sqrt{2}}\left(=\dfrac{1}{2}\right)\)
nên hệ phương trình có vô số nghiệm
\(\left\{{}\begin{matrix}x-3y=\sqrt{2}\\2x-6y=2\sqrt{2}\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x-3y=\sqrt{2}\\x-3y=\sqrt{2}\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}0y=0\\x-3y=\sqrt{2}\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}y\in R\\x=3y+\sqrt{2}\end{matrix}\right.\)
21: \(\left\{{}\begin{matrix}\dfrac{x}{2}-\dfrac{y}{3}=1\\-5x+8y=-3\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}3x-2y=6\\-5x+8y=-3\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}12x-8y=24\\-5x+8y=-3\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}7x=21\\3x-2y=6\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}x=3\\2y=3x-6=3\cdot3-6=9-6=3\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x=3\\y=\dfrac{3}{2}\end{matrix}\right.\)
22: \(\left\{{}\begin{matrix}\dfrac{x-1}{6}+\dfrac{2x-y}{4}=1\\\dfrac{x+y}{2}-\dfrac{y-x-1}{3}=2\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}2\left(x-1\right)+3\left(2x-y\right)=12\\3\left(x+y\right)-2\left(y-x-1\right)=12\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}2x-2+6x-3y=12\\3x+3y-2y+2x+2=12\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}8x-3y=14\\5x+y=10\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}8x-3y=14\\15x+3y=30\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}23x=44\\5x+y=10\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}x=\dfrac{44}{23}\\y=10-5x=10-5\cdot\dfrac{44}{23}=\dfrac{10}{23}\end{matrix}\right.\)
23:
\(\left\{{}\begin{matrix}3\left(x+1\right)+2\left(x+2y\right)=4\\4\left(x+1\right)-\left(x+2y\right)=9\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}3\left(x+1\right)+2\left(x+2y\right)=4\\8\left(x+1\right)-2\left(x+2y\right)=18\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}11\left(x+1\right)=22\\4\left(x+1\right)-\left(x+2y\right)=9\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}x+1=2\\x+2y=4\cdot2-9=-1\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x=1\\2y=-1-x=-2\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x=1\\y=-1\end{matrix}\right.\)