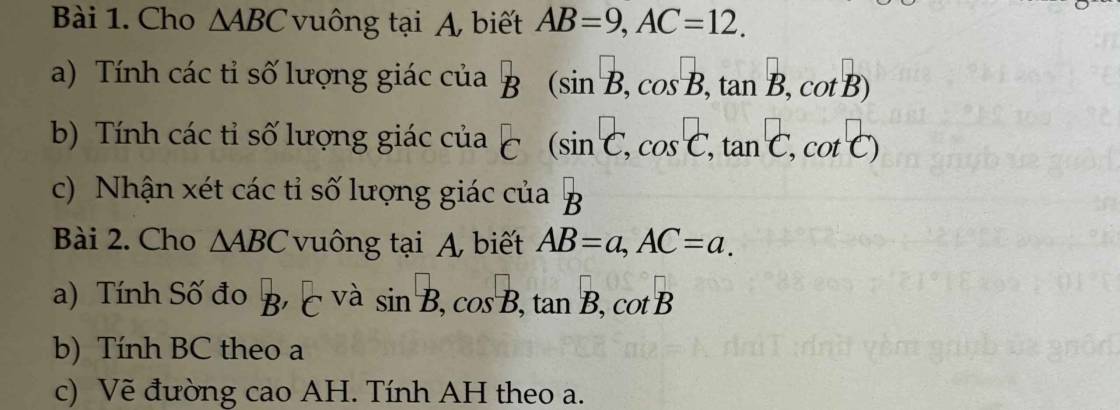Bài 2:
a: Xét ΔABC vuông tại A có \(tanB=\dfrac{AC}{AB}=1\)
=>\(\widehat{B}=45^0\)
=>\(cotB=cot45=1\)
Xét ΔABC vuông tại A có \(\widehat{B}+\widehat{C}=90^0\)
=>\(\widehat{C}=90^0-45^0=45^0\)
Xét ΔABC vuông tại A có
\(sinB=sin45=\dfrac{\sqrt{2}}{2};cosB=cos45=\dfrac{\sqrt{2}}{2}\)
b: ΔABC vuông tại A
=>\(AB^2+AC^2=BC^2\)
=>\(BC^2=a^2+a^2=2a^2\)
=>\(BC=a\sqrt{2}\)
c: Xét ΔABC vuông tại A có AH là đường cao
nên \(AH\cdot BC=AB\cdot AC\)
=>\(AH\cdot a\sqrt{2}=a\cdot a=a^2\)
=>\(AH=\dfrac{a^2}{a\sqrt{2}}=\dfrac{a\sqrt{2}}{2}\)
Bài 1:
a: ΔABC vuông tại A
=>\(BC^2=AB^2+AC^2\)
=>\(BC=\sqrt{9^2+12^2}=15\)
Xét ΔABC vuông tại A có
\(sinB=\dfrac{AC}{BC}=\dfrac{12}{15}=\dfrac{4}{5};cosB=\dfrac{AB}{BC}=\dfrac{9}{15}=\dfrac{3}{5}\)
\(tanB=\dfrac{sinB}{cosB}=\dfrac{4}{3};cotB=\dfrac{cosB}{sinB}=\dfrac{3}{4}\)
b: Xét ΔABC vuông tại A có
\(sinC=\dfrac{AB}{BC}=\dfrac{9}{15}=\dfrac{3}{5};cosC=\dfrac{AC}{BC}=\dfrac{12}{15}=\dfrac{4}{5}\)
\(tanC=\dfrac{AB}{AC}=\dfrac{9}{12}=\dfrac{3}{4};cotB=\dfrac{AC}{AB}=\dfrac{4}{3}\)
c: Nhận xét: \(\dfrac{3}{4}=0,75;\dfrac{3}{5}=0,6;\dfrac{4}{5}=0,8\)
Vì 0,6<0,75<0,8<4/3
nên \(cosB< cotB< sinB< tanB\)
Bài 4:
a: ΔAHB vuông tại H
=>\(HA^2+HB^2=AB^2\)
=>\(HB^2=15^2-12^2=81=9^2\)
=>HB=9(cm)
Xét ΔABC vuông tại A có AH là đường cao
nên \(AB^2=BH\cdot BC\)
=>\(BC=\dfrac{15^2}{9}=25\left(cm\right)\)
ΔABC vuông tại A
=>\(AB^2+AC^2=BC^2\)
=>\(AC=\sqrt{25^2-15^2}=20\left(cm\right)\)
Chu vi tam giác ABC là:
AB+AC+BC
=15+20+25
=60(cm)
b: Xét tứ giác ADHE có \(\widehat{ADH}=\widehat{AEH}=\widehat{DAE}=90^0\)
nên ADHE là hình chữ nhật
c: Xét ΔABC vuông tại A có \(cosB=\dfrac{AB}{BC};cosC=\dfrac{AC}{BC}\)
\(AB\cdot cosB+AC\cdot cosC=AB\cdot\dfrac{AB}{BC}+AC\cdot\dfrac{AC}{BC}\)
\(=\dfrac{AB^2+AC^2}{BC}=\dfrac{BC^2}{BC}=BC\)
d: Xét ΔAHB vuông tại H có \(sinB=\dfrac{AH}{AB}\)
Xét ΔAHC vuông tại H có \(sinC=\dfrac{AH}{AC}\)
Ta có: ADHE là hình chữ nhật
=>\(\widehat{ADE}=\widehat{AHE}\)
mà \(\widehat{AHE}=\widehat{ACB}\left(=90^0-\widehat{HAC}\right)\)
nên \(\widehat{ADE}=\widehat{ACB}\)
Xét ΔADE vuông tại A và ΔACB vuông tại A có
\(\widehat{ADE}=\widehat{ACB}\)
Do đó: ΔADE~ΔACB
=>\(\dfrac{S_{ADE}}{S_{ACB}}=\left(\dfrac{DE}{CB}\right)^2=\left(\dfrac{AH}{CB}\right)^2\)
\(sin^2B\cdot sin^2C=\left(\dfrac{AH}{AB}\right)^2\cdot\left(\dfrac{AH}{AC}\right)^2=\dfrac{AH^4}{\left(AB\cdot AC\right)^2}\)
\(=\dfrac{AH^4}{\left(AH\cdot BC\right)^2}=\dfrac{AH^2}{BC^2}=\left(\dfrac{AH}{BC}\right)^2=\dfrac{S_{ADE}}{S_{ACB}}\)
=>\(S_{ADE}=S_{ACB}\cdot sin^2B\cdot sin^2C\)