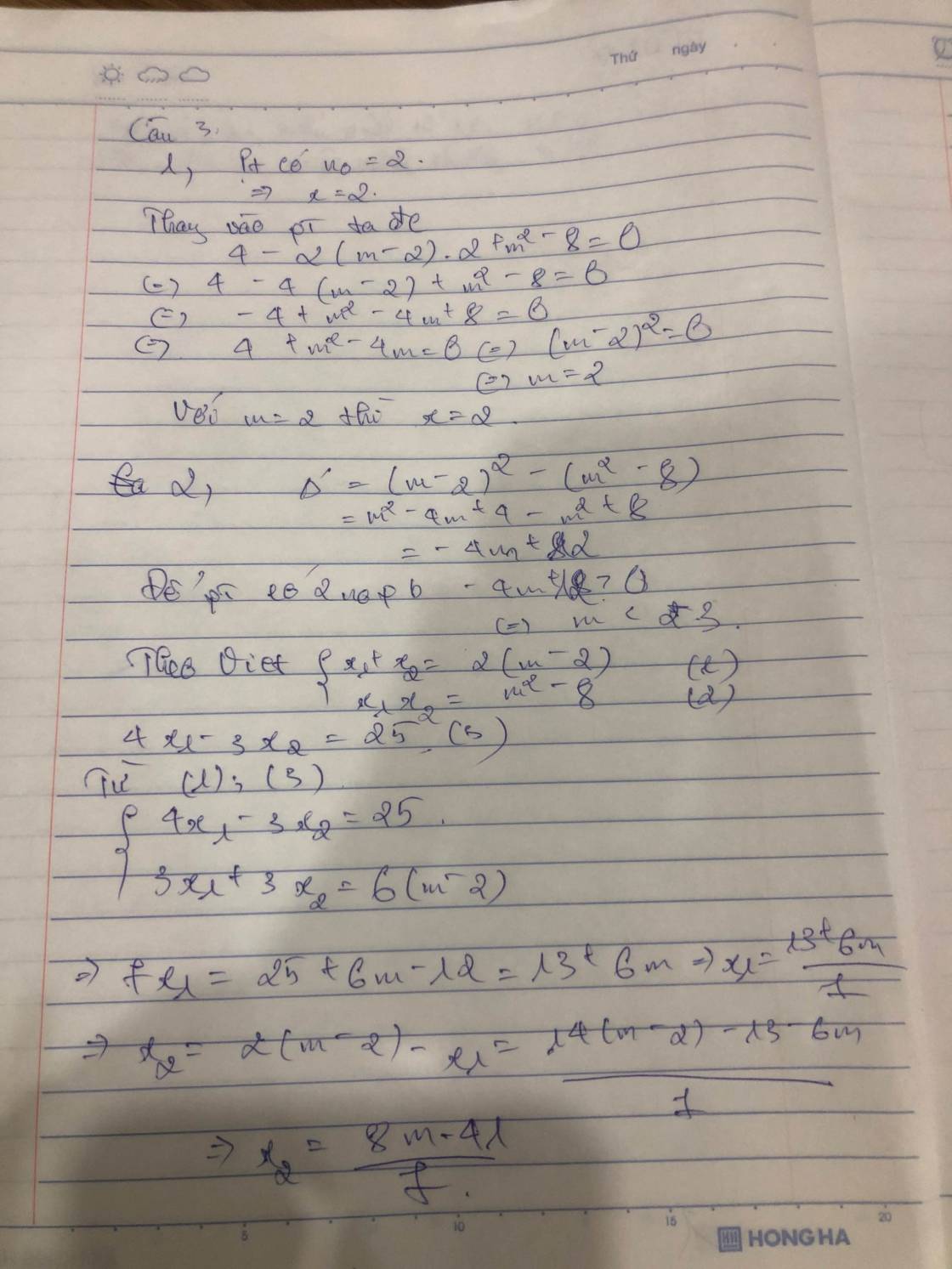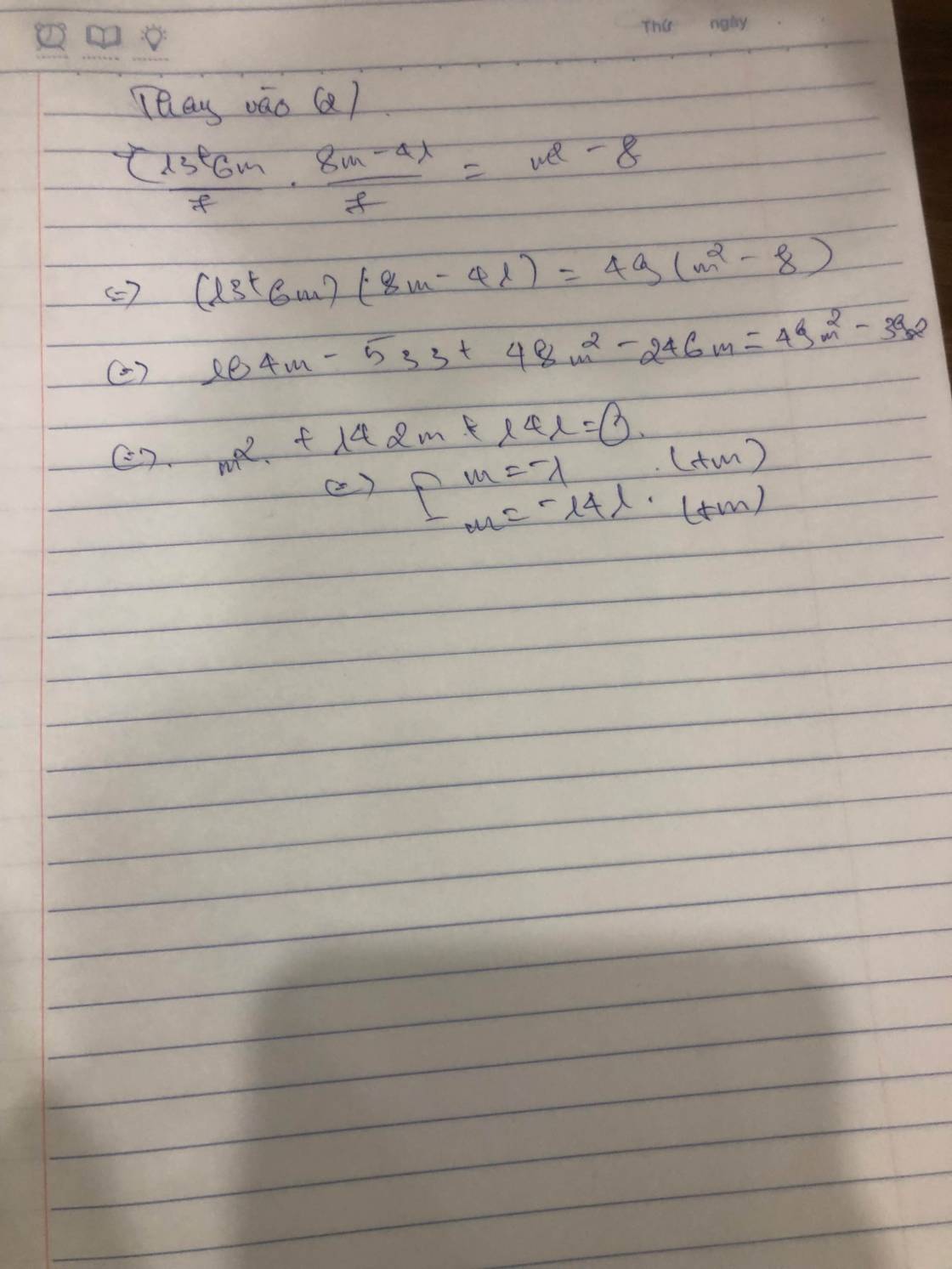1) Thay x = 2 vào PT ta có:
\(2^2-2\left(m-2\right)\cdot2+m^2-8=0\)
\(\Leftrightarrow4-4m+8+m^2-8=0\)
\(\Leftrightarrow m^2-4m+4=0\)
\(\Leftrightarrow\left(m-2\right)^2=0\)
\(\Leftrightarrow m=2\)
Vậy m = 2 là GT cần tìm
2)
\(\Delta'=\left[-\left(m-2\right)\right]^2-1\cdot\left(m^2-8\right)\)
\(=m^2-4m+4-m^2+8=-4m+12\)
Để PT có 2 nghiệm pb thì \(\Delta'>0\Leftrightarrow-4m+12>0\Leftrightarrow m< 3\)
Theo Vi-ét ta có:\(\left\{{}\begin{matrix}x_1+x_2=2\left(m-2\right)\left(1\right)\\x_1x_2=m^2-8\left(2\right)\end{matrix}\right.\)
Theo đề bài có: \(4x_1-3x_2=25\left(3\right)\)
Từ (1)(3) ta có HPT:\(\left\{{}\begin{matrix}x_1+x_2=2\left(m-2\right)\\4x_1-3x_2=25\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}3x_1+3x_2=6m-12\\4x_1-3x_2=25\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}7x_1=6m+13\\x_1+x_2=2\left(m-2\right)\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}x_1=\dfrac{6m+13}{7}\\\dfrac{6m+13}{7}+x_2=2m-4\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}x_1=\dfrac{6m+13}{7}\\x_2=\dfrac{8m-41}{7}\end{matrix}\right.\)
Thay x1, x2 vào (2) ta có:
\(\dfrac{6m+13}{7}\cdot\dfrac{8m-41}{7}=m^2-8\)
\(\Leftrightarrow\left(6m+13\right)\left(8m-41\right)=49m^2-392\)
\(\Leftrightarrow48m^2-142m-533=49m^2-392\)
\(\Leftrightarrow m^2+142m+141=0\)
Theo Vi-ét, \(a-b+c=1-142+141=0\)
\(\Rightarrow\left\{{}\begin{matrix}m=-1\\m=-141\end{matrix}\right.\)(T/m)
Vậy m = \(\left\{-1;-141\right\}\) là các GT cần tìm