a: Thay m=-1 vào (d), ta được:
y=(-1-2)x+3=-3x+3
Vẽ đồ thị:
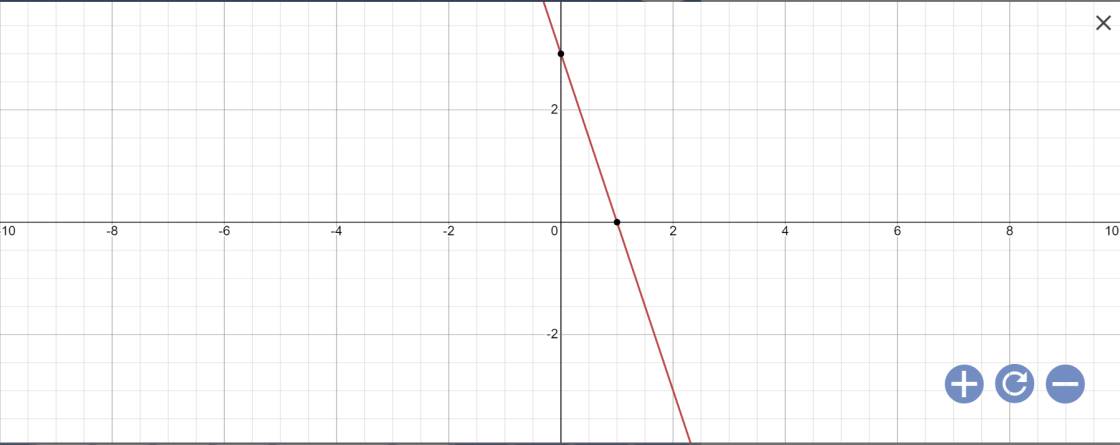
b: (d): y=(m-2)x+3
=>(m-2)x-y+3=0
Khoảng cách từ O đến (d) là:
\(d\left(O;\left(d\right)\right)=\dfrac{\left|0\left(m-2\right)+0\cdot\left(-1\right)+3\right|}{\sqrt{\left(m-2\right)^2+1}}=\dfrac{3}{\sqrt{\left(m-2\right)^2+1}}\)
Để d(O;(d))=1 thì \(\dfrac{3}{\sqrt{\left(m-2\right)^2+1}}=1\)
=>\(\sqrt{\left(m-2\right)^2+1}=3\)
=>\(\left(m-2\right)^2+1=9\)
=>\(\left(m-2\right)^2=8\)
=>\(m-2=\pm2\sqrt{2}\)
=>\(m=\pm2\sqrt{2}+2\)
c: Để OA=OB thì ΔOAB vuông cân tại O
=>\(\widehat{OAB}=45^0\)
=>\(tan\widehat{\left(d\right);Ox}=tan45=1\)
=>m-2=1
=>m=3














