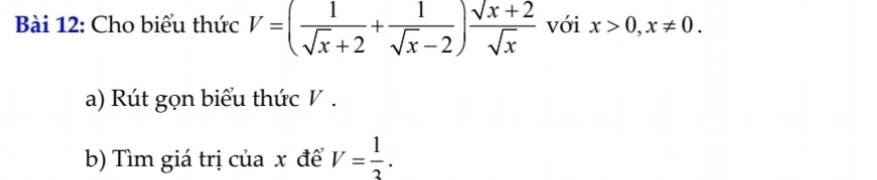\(a,V=\left(\dfrac{1.\left(\sqrt{x}-2\right)}{x-4}+\dfrac{\sqrt{x}+2}{x-4}\right).\dfrac{\sqrt{x}+2}{\sqrt{x}}\\ =\dfrac{\sqrt{x}-2+\sqrt{x}+2}{x-4}.\dfrac{\sqrt{x}+2}{\sqrt{x}}\\ =\dfrac{2\sqrt{x}}{x-4}.\dfrac{\sqrt{x}+2}{\sqrt{x}}\\ =\dfrac{2}{\sqrt{x}-2}\)
\(b.\dfrac{2}{\sqrt{x}-2}=\dfrac{1}{3}\\ \Leftrightarrow6=\sqrt{x}-2\\ \Leftrightarrow\sqrt{x}=8\\ \Leftrightarrow x=64\left(t/m\right)\)
Đúng 2
Bình luận (0)
