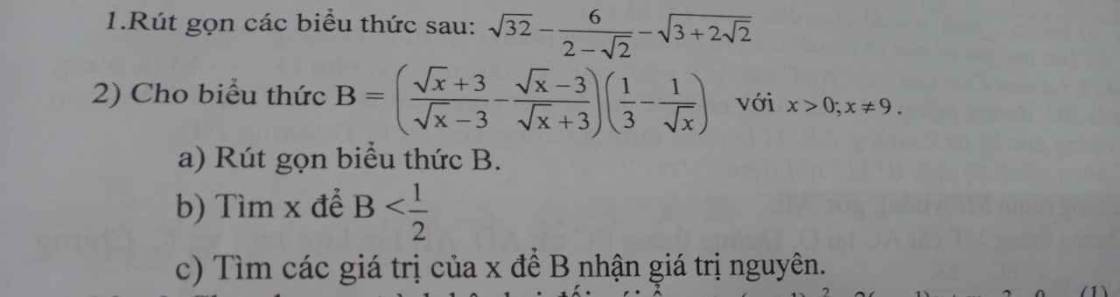1: \(\sqrt{32}-\dfrac{6}{2-\sqrt{2}}-\sqrt{3+2\sqrt{2}}\)
\(=4\sqrt{2}-\dfrac{6\left(2+\sqrt{2}\right)}{4-2}-\sqrt{\left(\sqrt{2}+1\right)^2}\)
\(=4\sqrt{2}-3\left(2+\sqrt{2}\right)-\left(\sqrt{2}+1\right)\)
\(=4\sqrt{2}-6-3\sqrt{2}-\sqrt{2}-1=-7\)
2:
a: \(B=\left(\dfrac{\sqrt{x}+3}{\sqrt{x}-3}-\dfrac{\sqrt{x}-3}{\sqrt{x}+3}\right)\left(\dfrac{1}{3}-\dfrac{1}{\sqrt{x}}\right)\)
\(=\dfrac{\left(\sqrt{x}+3\right)^2-\left(\sqrt{x}-3\right)^2}{\left(\sqrt{x}-3\right)\left(\sqrt{x}+3\right)}\cdot\dfrac{\sqrt{x}-3}{3\sqrt{x}}\)
\(=\dfrac{x+6\sqrt{x}+9-x+6\sqrt{x}-9}{\sqrt{x}+3}\cdot\dfrac{1}{3\sqrt{x}}=\dfrac{4}{\sqrt{x}+3}\)
b: \(B< \dfrac{1}{2}\)
=>\(\dfrac{4}{\sqrt{x}+3}-\dfrac{1}{2}< 0\)
=>\(\dfrac{8-\sqrt{x}-3}{2\left(\sqrt{x}+3\right)}< 0\)
=>\(5-\sqrt{x}< 0\)
=>\(\sqrt{x}>5\)
=>x>25
c: Để B là số nguyên thì \(4⋮\sqrt{x}+3\)
mà \(\sqrt{x}+3>=3\forall x\) thỏa mãn ĐKXĐ
nên \(\sqrt{x}+3=4\)
=>x=1(nhận)