Question

Answer 1

  

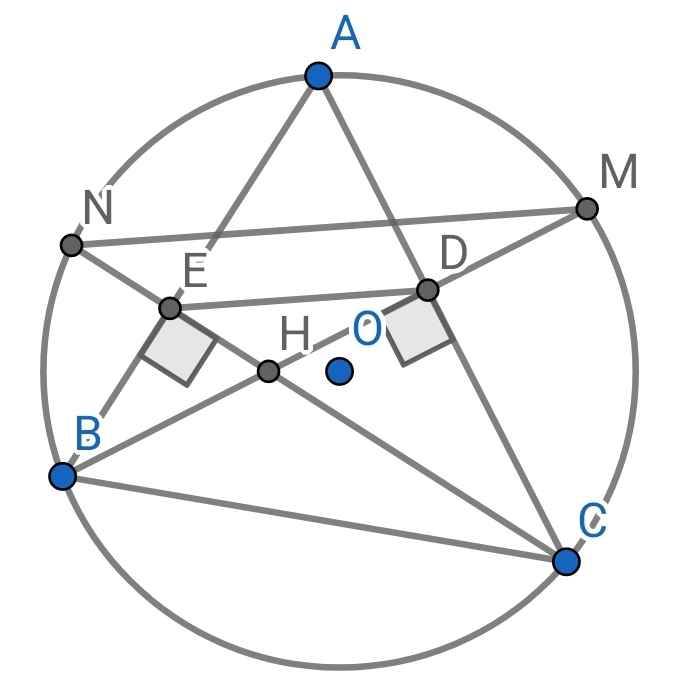
a) Xét tứ giác BEDC có:

∠BEC = ∠BDC = 90⁰ (gt)

⇒ D và E cùng nhìn cạnh BC dưới một góc 90⁰

⇒ BEDC nội tiếp

b) Do BEDC nội tiếp (cmt)

⇒ ∠EBD = ∠ECD (hai góc nội tiếp cùng chắn cung DE)

⇒ ∠ABM = ∠ACN

Mà ∠ABM là góc nội tiếp chắn cung AM của (O)

∠ACN là góc nội tiếp chắn cung AN

⇒ cung AM = cung AN

⇒ A là điểm chính giữa của cung MN

c) Do BEDC nội tiếp (cmt)

⇒ ∠BDE = ∠BCE (hai góc nội tiếp cùng chắn cung BE)

⇒ ∠BDE = ∠BCN

Mà ∠BCN = ∠BMN (hai góc nội tiếp cùng chắn cung BN của (O))

⇒ ∠BDE = ∠BMN

Mà ∠BDE và ∠BMN là hai góc đồng vị

⇒ DE // MN