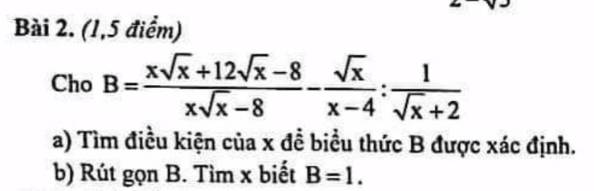a: ĐKXĐ: \(\left\{{}\begin{matrix}x>=0\\x\ne4\end{matrix}\right.\)
b: \(B=\dfrac{x\sqrt{x}+12\sqrt{x}-8}{x\sqrt{x}-8}-\dfrac{\sqrt{x}}{x-4}:\dfrac{1}{\sqrt{x}+2}\)
\(=\dfrac{x\sqrt{x}+12\sqrt{x}-8}{\left(\sqrt{x}-2\right)\left(x+2\sqrt{x}+4\right)}-\dfrac{\sqrt{x}}{x-4}\cdot\dfrac{\sqrt{x}+2}{1}\)
\(=\dfrac{x\sqrt{x}+12\sqrt{x}-8}{\left(\sqrt{x}-2\right)\left(x+2\sqrt{x}+4\right)}-\dfrac{\sqrt{x}}{\sqrt{x}-2}\)
\(=\dfrac{x\sqrt{x}+12\sqrt{x}-8-\sqrt{x}\left(x+2\sqrt{x}+4\right)}{\left(\sqrt{x}-2\right)\left(x+2\sqrt{x}+4\right)}\)
\(=\dfrac{x\sqrt{x}+12\sqrt{x}-8-x\sqrt{x}-2x-4\sqrt{x}}{\left(\sqrt{x}-2\right)\left(x+2\sqrt{x}+4\right)}\)
\(=\dfrac{-2x+8\sqrt{x}-8}{\left(\sqrt{x}-2\right)\left(x+2\sqrt{x}+4\right)}\)
\(=\dfrac{-2\left(x-4\sqrt{x}+4\right)}{\left(\sqrt{x}-2\right)\left(x+2\sqrt{x}+4\right)}=\dfrac{-2\left(\sqrt{x}-2\right)}{x+2\sqrt{x}+4}\)
Để B=1 thì \(-2\left(\sqrt{x}-2\right)=x+2\sqrt{x}+4\)
=>\(x+2\sqrt{x}+4=-2\sqrt{x}+4\)
=>\(x+4\sqrt{x}=0\)
=>\(\sqrt{x}\cdot\left(\sqrt{x}+4\right)=0\)
=>\(\sqrt{x}=0\)
=>x=0(nhận)