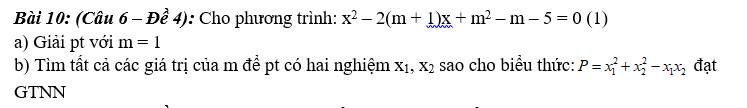a) \(x^2-2\left(m+1\right)x+m^2-m-5=0\) (1)
Thay m = 1 vào phương trình (1), ta được:
\(x^2-2\left(1+1\right)x+1^2-1-5=0\)
\(\Leftrightarrow x^2-4x-5=0\)
\(\Leftrightarrow x^2-5x+x-5=0\)
\(\Leftrightarrow x\left(x-5\right)+\left(x-5\right)=0\)
\(\Leftrightarrow\left(x+1\right)\left(x-5\right)=0\)
\(\Leftrightarrow\left[{}\begin{matrix}x+1=0\\x-5=0\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}x=-1\\x=5\end{matrix}\right.\)
b) \(\Delta=4\left(m+1\right)^2-4\left(m^2-m-5\right)=12m+24\)
Để phương trình có hai nghiệm thì: \(\Delta\ge0\Leftrightarrow m\ge-2\)
Theo hệ thức Vi-ét: \(\left\{{}\begin{matrix}x_1+x_2=2m+2\\x_1x_2=m^2-m-5\end{matrix}\right.\)
Khi đó: \(P=x_1^2+x_2^2-x_1x_2\)
\(=\left(x_1+x_2\right)^2-3x_1x_2\)
\(=\left(2m+2\right)^2-3\left(m^2-m-5\right)\)
\(=4m^2+8m+4-3m^2+3m+15\)
\(=m^2+11m+19\)
\(=\left[m^2+2\cdot m\cdot\dfrac{11}{2}+\left(\dfrac{11}{2}\right)^2\right]-\left(\dfrac{11}{2}\right)^2+19\)
\(=\left(m+\dfrac{11}{2}\right)^2-\dfrac{45}{4}\)
Ta thấy: \(\left(m+\dfrac{11}{2}\right)^2\ge0;\forall m\)
\(\Rightarrow\left(m+\dfrac{11}{2}\right)^2-\dfrac{45}{4}\ge-\dfrac{45}{4};\forall m\)
\(\Rightarrow P\ge-\dfrac{45}{4};\forall m\)
Dấu \("="\) xảy ra khi: \(m+\dfrac{11}{2}=0\Leftrightarrow m=-\dfrac{11}{2}\) (loại)
Vậy không tìm được giá trị nào của m thỏa mãn đề bài.
$\text{#}Toru$