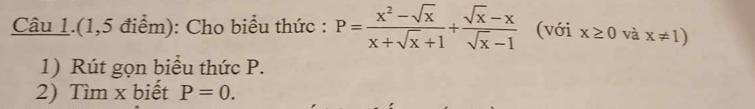a.
\(P=\dfrac{\sqrt{x}\left(x\sqrt{x}-1\right)}{x+\sqrt{x}+1}+\dfrac{-\sqrt{x}\left(\sqrt{x}-1\right)}{\sqrt{x}-1}\)
\(=\dfrac{\sqrt{x}\left(\sqrt{x}-1\right)\left(x+\sqrt{x}+1\right)}{x+\sqrt{x}+1}-\sqrt{x}\)
\(=\sqrt{x}\left(\sqrt{x}-1\right)-\sqrt{x}\)
\(=x-2\sqrt{x}\)
b.
\(P=0\Rightarrow x-2\sqrt{x}=0\)
\(\Rightarrow\sqrt{x}\left(\sqrt{x}-2\right)=0\)
\(\Rightarrow\left[{}\begin{matrix}\sqrt{x}=0\\\sqrt{x}=2\end{matrix}\right.\)
\(\Rightarrow\left[{}\begin{matrix}x=0\\x=4\end{matrix}\right.\)
Đúng 2
Bình luận (0)
