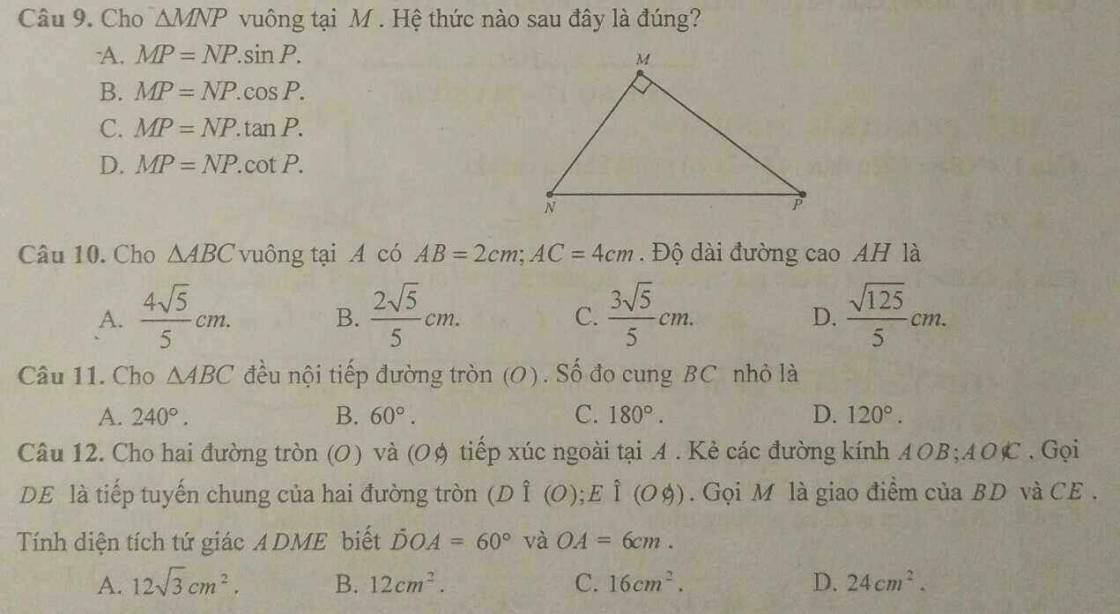Câu 9: B
Câu 10: ΔABC vuông tại A
=>\(AB^2+AC^2=BC^2\)
=>\(BC=\sqrt{2^2+4^2}=2\sqrt{5}\left(cm\right)\)
Xét ΔABC vuông tại A có AH là đường cao
nên \(AH\cdot BC=AB\cdot AC\)
=>\(AH\cdot2\sqrt{5}=2\cdot4=8\)
=>\(AH=\dfrac{8}{2\sqrt{5}}=\dfrac{4\sqrt{5}}{5}\left(cm\right)\)
=>Chọn A
Câu 11:
Xét (O) có
\(\widehat{BAC}\) là góc nội tiếp chắn cung CB
nên \(sđ\stackrel\frown{BC}_{nhỏ}=2\cdot\widehat{BAC}=120^0\)
=>Chọn D
Đúng 2
Bình luận (0)
