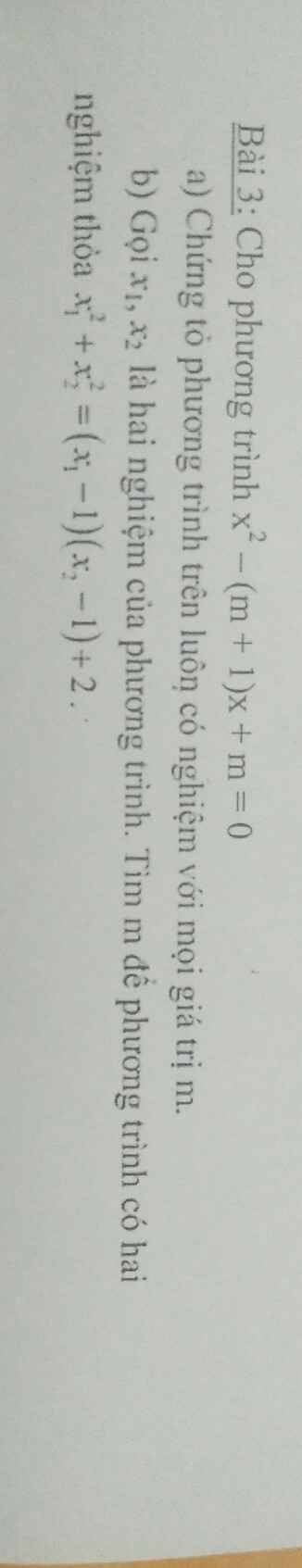Question

Answer 1

a.

\(\Delta=\left(m+1\right)^2-4m=m^2-2m+1=\left(m-1\right)^2\ge0;\forall m\)

\(\Rightarrow\) Phương trình luôn có nghiệm với mọi m

b.

Theo hệ thức Viet: \(\left\{{}\begin{matrix}x_1+x_2=m+1\\x_1x_2=m\end{matrix}\right.\)

\(x_1^2+x_2^2=\left(x_1-1\right)\left(x_2-1\right)+2\)

\(\Leftrightarrow\left(x_1+x_2\right)^2-2x_1x_2=x_1x_2-\left(x_1+x_2\right)+1+2\)

\(\Leftrightarrow\left(x_1+x_2\right)^2-3x_1x_2+\left(x_1+x_2\right)-3=0\)

\(\Leftrightarrow\left(m+1\right)^2-3m+\left(m+1\right)-3=0\)

\(\Leftrightarrow m^2-1=0\Rightarrow\left[{}\begin{matrix}m=1\\m=-1\end{matrix}\right.\)