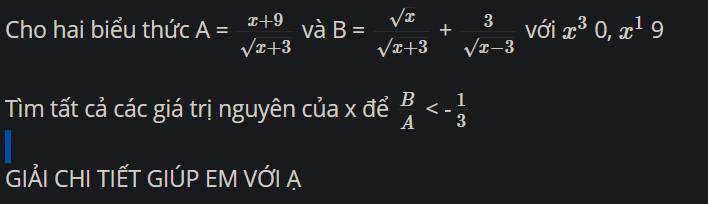\(\dfrac{B}{A}=\left(\dfrac{\sqrt{x}}{\sqrt{x}+3}+\dfrac{3}{\sqrt{x}-3}\right):\dfrac{x+9}{\sqrt{x}+3}\)
\(=\dfrac{\sqrt{x}\left(\sqrt{x}-3\right)+3\left(\sqrt{x}+3\right)}{\left(\sqrt{x}+3\right)\left(\sqrt{x}-3\right)}\cdot\dfrac{\sqrt{x}+3}{x+9}\)
\(=\dfrac{x-3\sqrt{x}+3\sqrt{x}+9}{\sqrt{x}-3}\cdot\dfrac{1}{x+9}=\dfrac{1}{\sqrt{x}-3}\)
Để B/A<-1/3 nên \(\dfrac{1}{\sqrt{x}-3}< -\dfrac{1}{3}\)
=>\(\dfrac{1}{\sqrt{x}-3}+\dfrac{1}{3}< 0\)
=>\(\dfrac{3+\sqrt{x}-3}{3\left(\sqrt{x}-3\right)}< 0\)
=>\(\dfrac{\sqrt{x}}{3\left(\sqrt{x}-3\right)}< 0\)
=>\(\sqrt{x}-3< 0\)
=>0<=x<9
Đúng 0
Bình luận (0)
