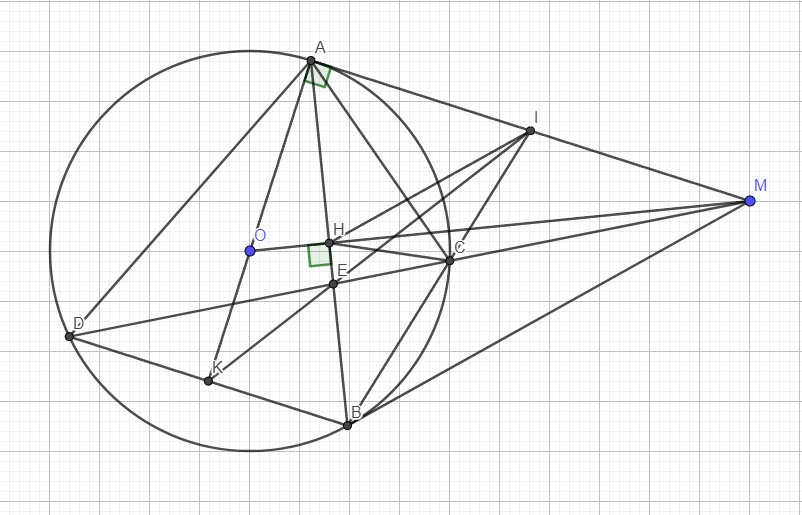
a.
Ta có \(MA=MB\) (t/c hai tiếp tuyến cắt nhau) và \(OA=OB=R\)
\(\Rightarrow OM\) là trung trực của AB
\(\Rightarrow OM\perp AB\) tại H và H là trung điểm AB
Xét hai tam giác AIC và BIA có:
\(\left\{{}\begin{matrix}\widehat{AIC}-chung\\\widehat{IAC}=\widehat{IBA}\left(\text{cùng chắn AC}\right)\end{matrix}\right.\)
\(\Rightarrow\Delta AIC\sim\Delta BIA\left(g.g\right)\) (1)
\(\Rightarrow\dfrac{IA}{IB}=\dfrac{IC}{IA}\Rightarrow IA^2=IB.IC\)
b.
Theo cm câu a, OM vuông góc AB tại H nên tam giác AHM vuông tại H
Trong tam giác AHM, HI là trung tuyến ứng với cạnh huyền \(\Rightarrow HI=\dfrac{1}{2}AM=AI\)
\(\Rightarrow\Delta IAH\) cân tại I \(\Rightarrow\widehat{AHI}=\widehat{HAI}\)
Mà từ (1) \(\Rightarrow\widehat{ACI}=\widehat{HAI}\) (2)
\(\Rightarrow\widehat{AHI}=\widehat{ACI}\)
Hai điểm H, C cùng nằm về 1 nửa mặt phẳng bờ AI \(\Rightarrow AHCI\) nội tiếp
Từ câu a, do \(IA^2=IB.IC\), mà \(IA=IM\) (I là trung điểm AM)
\(\Rightarrow IM^2=IB.IC\Rightarrow\dfrac{IM}{IB}=\dfrac{IC}{IM}\)
Lại có góc \(\widehat{MIC}\) chung \(\Rightarrow\Delta MIC\sim\Delta BIM\left(c.g.c\right)\)
\(\Rightarrow\widehat{IMC}=\widehat{IBM}\)
Mà \(\widehat{IBM}=\widehat{BDC}\) (cùng chắn BC)
\(\Rightarrow\widehat{IMC}=\widehat{BDC}\Rightarrow AM||BD\) (hai góc slt bằng nhau)
\(\Rightarrow\widehat{ABD}=\widehat{HAI}\) (so le trong) (3)
Lại có \(\widehat{ABD}=\widehat{ACD}\) (cùng chắn AD) (4)
Từ (2);(3);(4) \(\Rightarrow\widehat{ACD}=\widehat{ACI}\)
\(\Rightarrow CA\) là phân giác của \(\widehat{ICD}\)
c.
Ta có \(AK\perp AM\) (AM là tiếp tuyến)
Mà \(AM||BD\) (cmt)
\(\Rightarrow AK\perp BD\)
\(\Rightarrow K\) là trung điểm BD (đường kính vuông góc dây cung)
Gọi E là giao điểm MD và AB, F là giao điểm AB và IK.
Áp dụng định lý Thales:
\(\dfrac{EB}{EA}=\dfrac{BD}{AM}=\dfrac{2BK}{2AI}=\dfrac{BK}{AI}\)
\(\dfrac{FB}{FA}=\dfrac{BK}{AI}\)
\(\Rightarrow\dfrac{EB}{AE}=\dfrac{FB}{FA}\)
Mà E, F cùng thuộc AB \(\Rightarrow E\) trùng F
Hay 3 đường thẳng MD, AB, IK đồng quy tại E