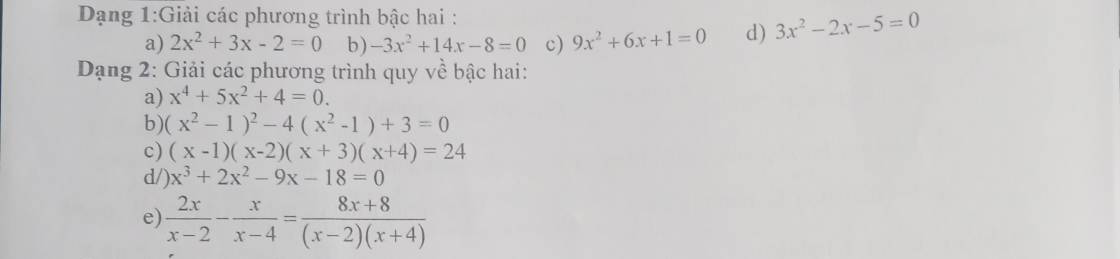Dạng 2:
a: \(x^4+5x^2+4=0\)
=>\(x^2\left(x^2+5\right)=-4\)
mà \(x^2\left(x^2+5\right)>=0>-4\forall x\)
nên \(x\in\varnothing\)
b: \(\left(x^2-1\right)^2-4\left(x^2-1\right)+3=0\)
=>\(\left(x^2-1\right)^2-\left(x^2-1\right)-3\left(x^2-1\right)+3=0\)
=>\(\left(x^2-1-1\right)\left(x^2-1-3\right)=0\)
=>\(\left(x^2-2\right)\left(x^2-4\right)=0\)
=>\(\left[{}\begin{matrix}x^2=2\\x^2=4\end{matrix}\right.\)
=>\(x\in\left\{2;-2;\sqrt{2};-\sqrt{2}\right\}\)
c: \(\left(x-1\right)\left(x-2\right)\left(x+3\right)\left(x+4\right)=24\)
=>\(\left(x-1\right)\left(x+3\right)\left(x-2\right)\left(x+4\right)=24\)
=>\(\left(x^2+2x-3\right)\left(x^2+2x-8\right)=24\)
=>\(\left(x^2+2x\right)^2-11\left(x^2+2x\right)=0\)
=>\(\left(x^2+2x\right)\left(x^2+2x-11\right)=0\)
=>\(x\in\left\{0;-2;-1+2\sqrt{3};-1-2\sqrt{3}\right\}\)
d: \(x^3+2x^2-9x-18=0\)
=>\(x^2\left(x+2\right)-9\left(x+2\right)=0\)
=>\(\left(x+2\right)\left(x^2-9\right)=0\)
=>(x+2)(x-3)(x+3)=0
=>\(x\in\left\{-2;3;-3\right\}\)
e: ĐKXĐ: \(x\notin\left\{2;4;-4\right\}\)
\(\dfrac{2x}{x-2}-\dfrac{x}{x-4}=\dfrac{8x+8}{\left(x-2\right)\left(x+4\right)}\)
=>\(\dfrac{2x\left(x-4\right)-x\left(x-2\right)}{\left(x-2\right)\left(x-4\right)}=\dfrac{8x+8}{\left(x-2\right)\left(x+4\right)}\)
=>\(\dfrac{x^2-6x}{\left(x-2\right)\left(x-4\right)}=\dfrac{8x+8}{\left(x-2\right)\left(x+4\right)}\)
=>\(\left(x^2-6x\right)\left(x+4\right)=\left(8x+8\right)\left(x-4\right)\)
=>\(x^3+4x^2-6x^2-24x=8x^2-32x+8x-32\)
=>\(x^3-2x^2-24x-8x^2+24x+32=0\)
=>\(x^3-10x^2+32=0\)
=>\(x^3-2x^2-8x^2+16x-16x+32=0\)
=>\(\left(x-2\right)\left(x^2-8x-16\right)=0\)
=>\(\left[{}\begin{matrix}x=2\left(loại\right)\\x^2-8x-16=0\end{matrix}\right.\)
=>\(\left[{}\begin{matrix}x=4+4\sqrt{2}\left(nhận\right)\\x=4-4\sqrt{2}\left(nhận\right)\end{matrix}\right.\)
Dạng 1:
a: \(2x^2+3x-2=0\)
=>\(2x^2+4x-x-2=0\)
=>(x+2)(2x-1)=0
=>\(\left[{}\begin{matrix}x=-2\\x=\dfrac{1}{2}\end{matrix}\right.\)
b: \(-3x^2+14x-8=0\)
=>\(3x^2-14x+8=0\)
=>\(3x^2-12x-2x+8=0\)
=>3x(x-4)-2(x-4)=0
=>(x-4)(3x-2)=0
=>\(\left[{}\begin{matrix}x=4\\x=\dfrac{2}{3}\end{matrix}\right.\)
c: \(9x^2+6x+1=0\)
=>\(\left(3x+1\right)^2=0\)
=>3x+1=0
=>x=-1/2
d: \(3x^2-2x-5=0\)
=>\(3x^2+3x-5x-5=0\)
=>(x+1)(3x-5)=0
=>\(\left[{}\begin{matrix}x=-1\\x=\dfrac{5}{3}\end{matrix}\right.\)