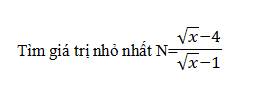Question

Answer 1

Ta có: \(N=\dfrac{\sqrt{x}-4}{\sqrt{x}-1}\left(x\ge0\right)\)

\(=\dfrac{\sqrt{x}-1-3}{\sqrt{x}-1}=\dfrac{\sqrt{x}-1}{\sqrt{x}-1}-\dfrac{3}{\sqrt{x}-1}\)

\(=1-\dfrac{3}{\sqrt{x}-1}\) 

\(\sqrt{x}\ge0\forall x\ge0\)

\(\Rightarrow\sqrt{x}-1\ge-1\forall x\ge0\)

\(\Rightarrow\dfrac{3}{\sqrt{x}-1}\le-3\forall x\ge0\)

\(\Rightarrow1-\dfrac{3}{\sqrt{x}-1}\ge1+3=4\Rightarrow N\ge4\forall x\ge0\)

Dấu "=" xảy ra khi: \(\sqrt{x}=0\Leftrightarrow x=0\left(tm\right)\)    

Vậy: ...