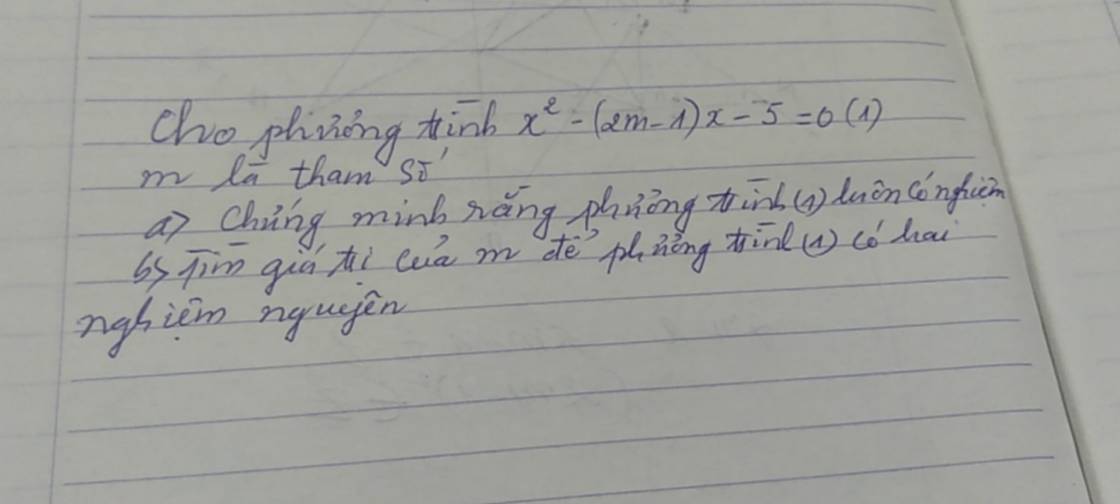a.
\(\Delta=\left(2m-1\right)^2+20>0;\forall m\Rightarrow\) pt luôn có 2 nghiệm pb với mọi m
b.
Pt đã cho có nghiệm nguyên khi \(\Delta\) là số chính phương
Đặt \(2m-1=n\in Z\Rightarrow\Delta=n^2+20\) là SCP
\(\Rightarrow n^2+20=k^2\) (với k là số nguyên)
\(\Leftrightarrow k^2-n^2=20\)
\(\Leftrightarrow\left(k-n\right)\left(k+n\right)=20\)
Do \(\left(k-n\right)+\left(k+n\right)=2k\) luôn chẵn nên chúng cùng tính chẵn lẻ
Mà tích của chúng là 20 chẵn \(\Rightarrow\) cả k-n và k+n đều chẵn
Do đó ta chỉ cần xét các cặp ước chẵn của 20:
| k-n | -10 | -2 | 2 | 10 |
| k+n | -2 | -10 | 10 | 2 |
| k | -6 | -6 | 6 | 6 |
| n | 4 | -4 | 4 | -4 |
\(\Rightarrow\left[{}\begin{matrix}2m-1=4\\2m-1=-4\end{matrix}\right.\) \(\Rightarrow\left[{}\begin{matrix}m=\dfrac{5}{2}\\m=-\dfrac{3}{2}\end{matrix}\right.\)