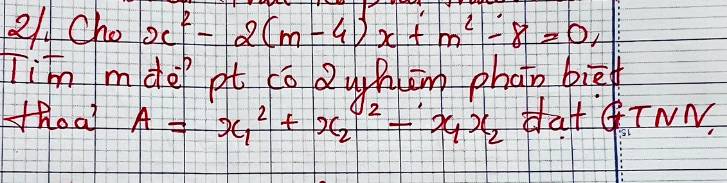\(\Delta'=\left(m-4\right)^2-\left(m^2-8\right)=-8m+24\)
Pt có 2 nghiệm pb khi \(-8m+24>0\Rightarrow m< 3\)
Khi đó theo hệ thức Viet: \(\left\{{}\begin{matrix}x_1+x_2=2\left(m-4\right)\\x_1x_2=m^2-8\end{matrix}\right.\)
\(A=x_1^2+x_2^2-x_1x_2=x_1^2+x_2^2+2x_1x_2-3x_1x_2\)
\(=\left(x_1+x_2\right)^2-3x_1x_2\)
\(=4\left(m-4\right)^2-3\left(m^2-8\right)\)
\(=m^2-32m+88\)
Đề bài ko đúng rồi em, biểu thức này ko có min với \(m< 3\)
Để có min thì yêu cầu của đề cần phải là "phương trình có 2 nghiệm" (bỏ 2 chữ phân biệt đi, khi đó min sẽ rơi vào m=3)
Đúng 0
Bình luận (1)
