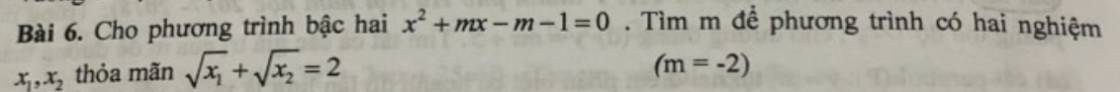\(\Delta=m^2-4\cdot1\cdot\left(-m-1\right)=m^2+4m+4=\left(m+2\right)^2\ge0\forall m\)
\(\Rightarrow\) PT luôn có nghiệm
Theo Vi-ét ta có:\(\left\{{}\begin{matrix}x_1+x_2=-m\\x_1\cdot x_2=-m-1\end{matrix}\right.\)
Theo đề bài ta có:\(\sqrt{x_1}+\sqrt{x_2}=2\)
\(\Leftrightarrow x_1+2\sqrt{x_1x_2}+x_2=4\)
\(\Leftrightarrow-m+2\sqrt{-m-1}=4\)
\(\Leftrightarrow2\sqrt{-m-1}=m+4\)
\(\Leftrightarrow\sqrt{-m-1}=\dfrac{m+4}{2}\)
\(\Leftrightarrow-m-1=\dfrac{m^2+8m+16}{4}\)
\(\Leftrightarrow-4m-4=m^2+8m+16\)
\(\Leftrightarrow m^2+12m+20=0\)
\(\Leftrightarrow\left(m+2\right)\left(m+10\right)=0\)
\(\Leftrightarrow\left[{}\begin{matrix}m=-2\\m=-10\end{matrix}\right.\)
Thay m= -2 vào PT \(-m+2\sqrt{-m-1}\) ta có
\(2+2\sqrt{1}=4\) (T/m)
Thay m= -10 vào PT \(-m+2\sqrt{-m-1}\)
\(10+2\sqrt{9}=10+6=16\) (Loại)