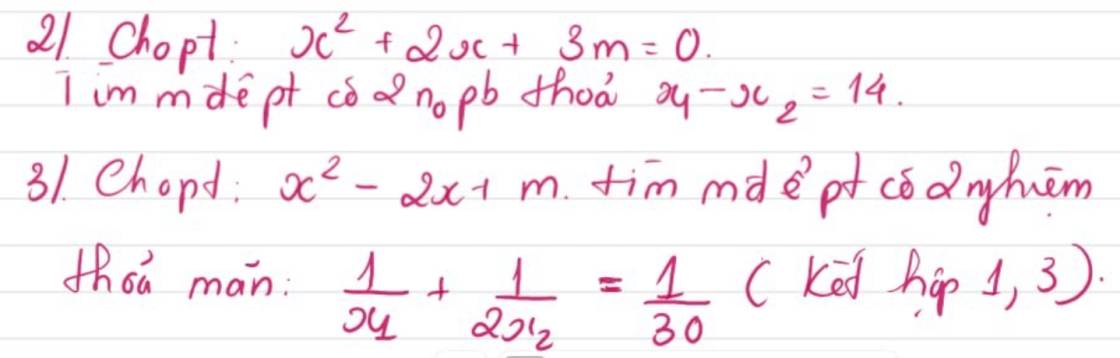2)
\(\Delta=2^2-4\cdot1\cdot3m=4-12m\)
PT có 2 nghiệm pb \(\Leftrightarrow4-12m>0\Leftrightarrow m< \dfrac{1}{3}\)
Theo Vi-ét và đề bài có:\(\left\{{}\begin{matrix}x_1+x_2=-2\left(1\right)\\x_1\cdot x_2=3m\left(2\right)\\x_1-x_2=14\left(3\right)\end{matrix}\right.\)
Từ (1)(3) ta có: \(\left\{{}\begin{matrix}x_1+x_2=-2\\x_1-x_2=14\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}2x_1=12\\x_1+x_2=-2\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}x_1=6\\x_2=-8\end{matrix}\right.\)
Thay x1, x2 vào (2) ta có:
\(6\cdot\left(-8\right)=3m\Leftrightarrow3m=-14\Leftrightarrow m=-\dfrac{14}{3}\) (T/m)
3)
\(\Delta=\left(-2\right)^2-4\cdot1\cdot m=4-4m\)
PT có nghiệm \(\Leftrightarrow4-4m\ge0\Leftrightarrow m\le1\)
Theo Vi-ét và đề bài ta có:\(\left\{{}\begin{matrix}x_1+x_2=2\left(1\right)\\x_1\cdot x_2=m\left(2\right)\\\dfrac{1}{x_1}+\dfrac{1}{2x_2}=\dfrac{1}{30}\left(3\right)\end{matrix}\right.\)
Từ (1)(3) ta có:\(\left\{{}\begin{matrix}x_1+x_2=2\\\dfrac{1}{x_1}+\dfrac{1}{2x_2}=\dfrac{1}{30}\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}x_1+x_2=2\\\dfrac{x_1+2x_2}{2x_1x_2}=\dfrac{1}{30}\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}x_1+x_2=2\\x_1x_2=15x_1+30x_2\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}30x_1+30x_2=60\\15x_1+30x_2=m\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}15x_1=60-m\\x_1+x_2=2\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}x_1=\dfrac{60-m}{15}\\x_2=2-\dfrac{60-m}{15}=\dfrac{m-30}{15}\end{matrix}\right.\)
Thay x1, x2 vào (2) ta có:
\(\dfrac{60-m}{15}\cdot\dfrac{m-30}{15}=m\)
\(\Leftrightarrow\dfrac{-m^2+90m-1800}{225}=\dfrac{225m}{225}\)
\(\Leftrightarrow m^2-90m+1800+225m=0\)
\(\Leftrightarrow m^2+135m+1800=0\)
\(\Leftrightarrow\left(m+120\right)\left(m+15\right)=0\)
\(\Leftrightarrow\left[{}\begin{matrix}m=-120\\m=-15\end{matrix}\right.\)(T/m)