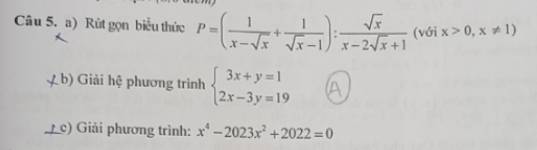a: \(P=\left(\dfrac{1}{x-\sqrt{x}}+\dfrac{1}{\sqrt{x}-1}\right):\dfrac{\sqrt{x}}{x-2\sqrt{x}+1}\)
\(=\left(\dfrac{1}{\sqrt{x}\left(\sqrt{x}-1\right)}+\dfrac{1}{\sqrt{x}-1}\right):\dfrac{\sqrt{x}}{\left(\sqrt{x}-1\right)^2}\)
\(=\dfrac{1+\sqrt{x}}{\sqrt{x}\left(\sqrt{x}-1\right)}\cdot\dfrac{\left(\sqrt{x}-1\right)^2}{\sqrt{x}}\)
\(=\dfrac{\left(1+\sqrt{x}\right)\left(1-\sqrt{x}\right)}{x}=\dfrac{1-x}{x}\)
b: \(\left\{{}\begin{matrix}3x+y=1\\2x-3y=19\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}9x+3y=3\\2x-3y=19\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}11x=22\\3x+y=1\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}x=2\\y=1-3x=1-3\cdot2=-5\end{matrix}\right.\)
c: \(x^4-2023x^2+2022=0\)
=>\(\left(x^2-1\right)\left(x^2-2022\right)=0\)
=>\(\left[{}\begin{matrix}x^2-1=0\\x^2-2022=0\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}x^2=1\\x^2=2022\end{matrix}\right.\)
=>\(\left[{}\begin{matrix}x=1\\x=-1\\x=\sqrt{2022}\\x=-\sqrt{2022}\end{matrix}\right.\)