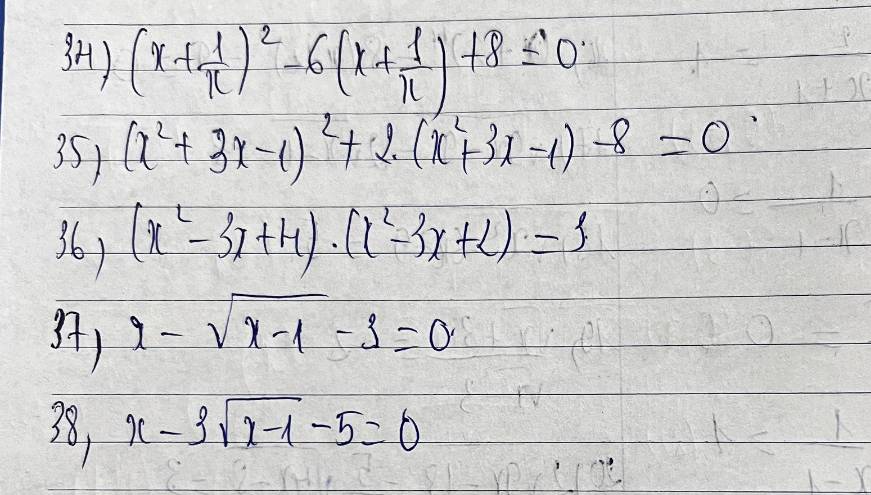Question

Answer 1

34. ĐKXĐ: $x\neq 0$

Đặt $x+\frac{1}{x}=a$ thì pt trở thành:

$a^2-6a+8=0$

$\Leftrightarrow (a-2)(a-4)=0$

$\Leftrightarrow a-2=0$ hoặc $a-4=0$

$\Leftrightarrow a=2$ hoặc $a=4$

Nếu $a=2$

$\Leftrightarrow x+\frac{1}{x}-2=0$

$\Leftrightarrow \frac{x^2-2x+1}{x}=0$

$\Rightarrow x^2-2x+1=0$

$\Leftrightarrow (x-1)^2=0\Leftrightarrow x=1$ (tm)

Nếu $a=4$

$\Leftrightarrow x+\frac{1}{x}-4=0$

$\Leftrightarrow \frac{x^2-4x+1}{x}=0$

$\Rightarrow x^2-4x+1=0$

$\Leftrightarrow (x-2)^2-3=0$

$\Leftrightarrow x-2=\pm \sqrt{3}$

$\Leftrightarrow x=2\pm \sqrt{3}$ (tm)

Answer 2

35.

Đặt $x^2+3x-1=a$. Khi đó pt trở thành:

$a^2+2a-8=0$

$\Leftrightarrow (a-2)(a+4)=0$

$\Leftrightarrow a-2=0$ hoặc $a+4=0$

Nếu $a-2=0$

$\Leftrightarrow x^2+3x-3=0$

$\Leftrightarrow (x+1,5)^2-5,25=0$

$\Leftrightarrow (x+1,5)^2=5,25$
$\Leftrightarrow x+1,5=\pm \sqrt{5,25}$

$\Leftrightarrow x=-1,5\pm \sqrt{5,25}$ (tm)

Nếu $a+4=0$

$\Leftrightarrow x^2+3x+3=0$

$\Leftrightarrow (x+1,5)^2+0,75=0$

$\Leftrightarrow (x+1,5)^2=-0,75<0$ (vô lý -loại)

Vậy../////////

Answer 3

36.

$(x^2-3x+4)(x^2-3x+2)=3$
Đặt $x^2-3x+2=a$. Khi đó pt trở thành:
$(a+2)a=3$

$\Leftrightarrow a^2+2a-3=0$

$\Leftrightarrow (a-1)(a+3)=0$

$\Leftrightarrow a-1=0$ hoặc $a+3=0$

Nếu $a-1=0$

$\Leftrightarrow x^2-3x+1=0$

$\Leftrightarrow (x-1,5)^2-1,25=0$

$\Leftrightarrow x-1,5=\pm \sqrt{1,25}$

$\Leftrightarrow x=1,5\pm \sqrt{1,25}$

Nếu $a+3=0$

$\Leftrightarrow x^2-3x+5=0$

$\Leftrightarrow (x-1,5)^2+2,75=0$

$\Leftrightarrow (x-1,5)^2=-2,75<0$ (vô lý - loại)

Vậy...........

Answer 4

38. ĐKXĐ: $x\geq 1$

Đặt $\sqrt{x-1}=a(a\geq 0)$. Khi đó: $x=a^2+1$. PT trở thành:

$a^2+1-3a-5=0$

$\Leftrightarrow a^2-3a-4=0$

$\Leftrightarrow (a+1)(a-4)=0$

$\Leftrightarrow a+1=0$ hoặc $a-4=0$

Nếu $a+1=0\Leftrightarrow a=-1<0$ (loại do $a\geq 0$)

Nếu $a-4=0\Leftrightarrow a=4$

$\Leftrightarrow \sqrt{x-1}=4\Leftrightarrow x-1=16$

$\Leftrightarrow x=17$.

Answer 5

37. ĐKXĐ: $x\geq 1$

Đặt $\sqrt{x-1}=a(a\geq 0)$. Khi đó $x=a^2+1$. PT trở thành:
$a^2+1-a-3=0$

$\Leftrightarrow a^2-a-2=0$

$\Leftrightarrow (a+1)(a-2)=0$
$\Leftrightarrow a+1=0$ hoặc $a-2=0$

Nếu $a+1=0\Leftrightarrow a=-1<0$ (loại do $a\geq 0$)

Nếu $a-2=0$

$\Leftrightarrow \sqrt{x-1}=2\Leftrightarrow x-1=4\Leftrightarrow x=5$ (tm)