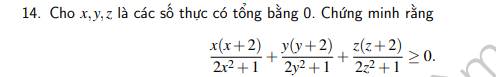\(\Leftrightarrow\dfrac{2x\left(x+2\right)}{2x^2+1}+\dfrac{2y\left(y+2\right)}{2y^2+1}+\dfrac{2z\left(z+2\right)}{2z^2+1}\ge0\)
\(\Leftrightarrow\dfrac{2x\left(x+2\right)}{2x^2+1}+1+\dfrac{2y\left(y+2\right)}{2y^2+1}+1+\dfrac{2z\left(z+2\right)}{2z^2+1}+1\ge3\)
\(\Leftrightarrow P=\dfrac{\left(2x+1\right)^2}{2x^2+1}+\dfrac{\left(2y+1\right)^2}{2y^2+1}+\dfrac{\left(2z+1\right)^2}{2z^2+1}\ge3\)
Ta có:
\(2x^2=\dfrac{4}{3}x^2+\dfrac{2}{3}x^2=\dfrac{4}{3}x^2+\dfrac{2}{3}\left(y+z\right)^2\le\dfrac{4}{3}\left(x^2+y^2+z^2\right)\)
Tương tự: \(2y^2\le\dfrac{4}{3}\left(x^2+y^2+z^2\right)\) ; \(2z^2\le\dfrac{4}{3}\left(x^2+y^2+z^2\right)\)
\(\Rightarrow P\ge\dfrac{\left(2x+1\right)^2+\left(2y+1\right)^2+\left(2z+1\right)^2}{\dfrac{4}{3}\left(x^2+y^2+z^2\right)+1}=\dfrac{4\left(x^2+y^2+z^2\right)+3}{\dfrac{4}{3}\left(x^2+y^2+z^2\right)+1}=3\) (đpcm)
Dấu "=" xảy ra khi \(\left(x;y;z\right)=\left(0;0;0\right);\left(-\dfrac{1}{2};-\dfrac{1}{2};1\right)\) và các hoán vị