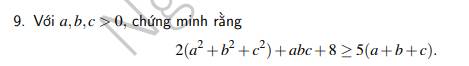Trong 3 số a;b;c luôn có ít nhất 2 số cùng phía so với 1, không mất tính tổng quát giả sử đó là a và b
\(\Rightarrow\left(a-1\right)\left(b-1\right)\ge0\Rightarrow ab\ge a+b-1\)
\(\Rightarrow abc\ge ac+bc-c\Rightarrow2abc\ge2ac+2bc-2c\)
\(\Rightarrow a^2+b^2+c^2+2abc+1\ge2ab+2ac+2bc+\left(c-1\right)^2\ge2ab+2bc+2ca\)
\(\Rightarrow2\left(a^2+b^2+c^2\right)+2abc+1\ge\left(a+b+c\right)^2\)
\(\Rightarrow2\left(a^2+b^2+c^2\right)+2abc+10\ge\left(a+b+c\right)^2+9\ge6\left(a+b+c\right)\) (1)
Lại có:
\(2\left(a^2+1\right)+2\left(b^2+1\right)+2\left(c^2+1\right)\ge4\left(a+b+c\right)\) (2)
Cộng vế (1) và (2):
\(4\left(a^2+b^2+c^2\right)+2abc+16\ge10\left(a+b+c\right)\)
Dấu "=" xảy ra khi \(a=b=c=1\)