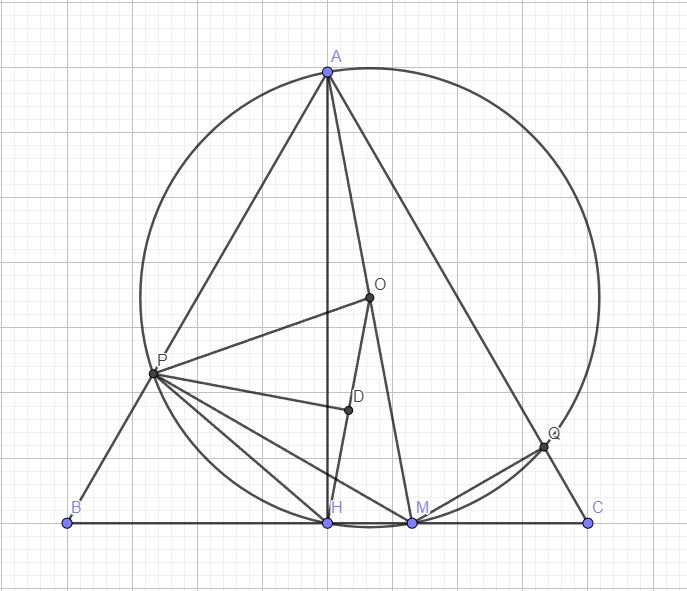
a.
Theo giả thiết \(\widehat{AHM}=\widehat{APM}=\widehat{AQM}=90^0\)
\(\Rightarrow\) H, P, Q cùng nhìn AM dưới 1 góc vuông
\(\Rightarrow\) A, P, M, H, Q cùng thuộc đường tròn đường kính AM
Do O là trung điểm AM \(\Rightarrow O\) là tâm đường tròn nói trên.
Gọi bán kính đường tròn là R.
b.
Tam giác ABC đều và AH là đường cao nên đồng thời là phân giác góc A
\(\Rightarrow\widehat{PAH}=\dfrac{1}{2}\widehat{A}=30^0\)
Mà \(\widehat{POH}=2\widehat{PAH}\) (góc ở tâm gấp đôi góc nt cùng chắn 1 cung)
\(\Rightarrow\widehat{POH}=60^0\)
Theo cm câu a, P, H cùng thuộc đường tròn nên \(OP=OH=R\)
\(\Rightarrow\Delta OPH\) cân tại O \(\Rightarrow\Delta OPH\) là tam giác đều (tam giác cân có 1 góc 60 độ)
\(\Rightarrow OP=OH=PH\)
Chứng minh tương tự ta có tam giác OQH đều \(\Rightarrow OQ=OH=QH\)
\(\Rightarrow OP=PH=HQ=OQ\) nên OPHQ là hình thoi
c.
Gọi D là trung điểm OH, theo cmt ta có tam giác OPH đều
\(\Rightarrow PD\perp OH\Rightarrow\Delta OPD\) vuông tại D
\(\Rightarrow PD=OP.sin\widehat{POH}=R.sin60^0=\dfrac{R\sqrt{3}}{2}\)
Do OPHQ là hình thoi \(\Rightarrow PQ=2PD=R\sqrt{3}\)
\(\Rightarrow PQ\) nhỏ nhất khi R nhỏ nhất
Mà AM là đường kính \(\Rightarrow AM=2R\Rightarrow PQ\) nhỏ nhất khi AM nhỏ nhất
\(\Rightarrow\) M là hình chiếu vuông góc của A lên BC
\(\Rightarrow M\) trùng H
Vậy khi M là trung điểm BC thì PQ có độ dài nhỏ nhất