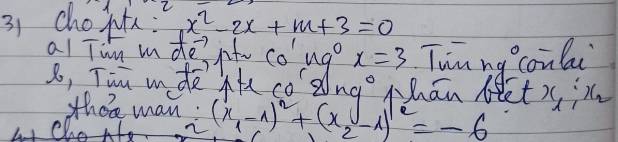Question

Answer 1

a: Thay x=3 vào phương trình, ta được:

\(3^2-2\cdot3+m+3=0\)

=>m+9+3-6=0

=>m+6=0

=>m=-6

Theo Vi-et, ta có: \(x_1+x_2=-\dfrac{b}{a}=2\)

=>\(x_2+3=2\)

=>\(x_2=-1\)

b: \(\text{Δ}=\left(-2\right)^2-4\left(m+3\right)=4-4m-12=-4m-8\)

Để phương trình có hai nghiệm phân biệt thì Δ>0

=>-4m-8>0

=>m+2<0

=>m<-2

Theo Vi-et, ta có:

\(x_1+x_2=-\dfrac{b}{a}=2;x_1x_2=\dfrac{c}{a}=m+3\)

\(\left(x_1-1\right)^2+\left(x_2-1\right)^2=-6\)

=>\(\left(x_1^2+x_2^2\right)-2\left(x_1+x_2\right)+2+6=0\)

=>\(\left(x_1+x_2\right)^2-2x_1x_2-2\left(x_1+x_2\right)+8=0\)

=>\(2^2-2\left(m+3\right)-2\cdot2+8=0\)

=>\(-2\left(m+3\right)=-8\)

=>m+3=4

=>m=1(loại)