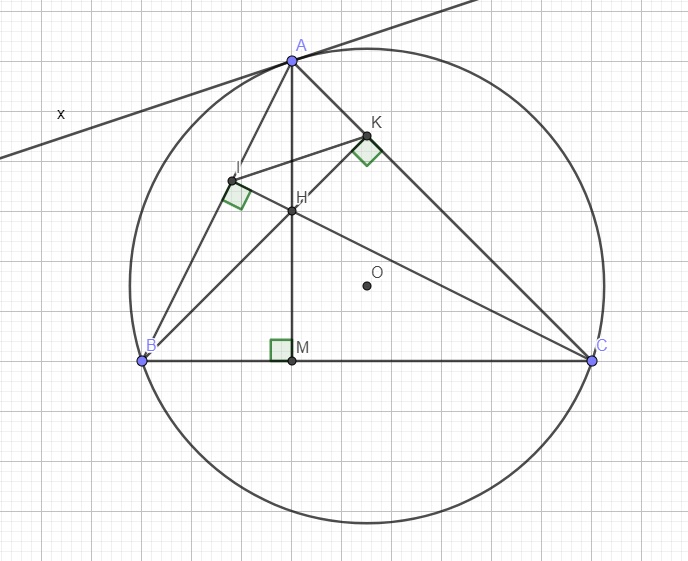
a.
Câu này đơn giản, em tự làm
b.
Do BIKC nội tiếp \(\Rightarrow\widehat{IKC}+\widehat{ABC}=180^0\)
Mà \(\widehat{IKC}+\widehat{AKI}=180^0\) (hai góc kề bù)
\(\Rightarrow\widehat{AKI}=\widehat{ABC}\)
c.
Xét hai tam giác AIK và ACB có:
\(\left\{{}\begin{matrix}\widehat{BAC}\text{ chung}\\\widehat{AKI}=\widehat{ABC}\left(cmt\right)\end{matrix}\right.\) \(\Rightarrow\Delta AIK\sim\Delta ACB\left(g.g\right)\)
d.
Từ câu c ta suy ra \(\widehat{ACB}=\widehat{AIK}\)
Mặt khác do Ax là tiếp tuyến \(\Rightarrow\widehat{BAx}=\widehat{ACB}\) (cùng chắn AB)
\(\Rightarrow\widehat{BAx}=\widehat{AIK}\)
\(\Rightarrow Ax||IK\) (hai góc so le trong bằng nhau)
e.
Do Ax là tiếp tuyến tại A \(\Rightarrow OA\perp Ax\)
Mà \(Ax||IK\) (cmt)
\(\Rightarrow OA\perp IK\)