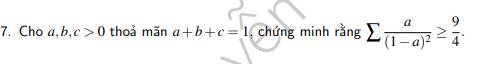Lời giải:
Áp dụng BĐT Cauchy-Schwarz:
\(\sum \frac{a}{(1-a)^2}=\sum \frac{a}{(b+c)^2}=\sum \frac{(\frac{a}{b+c})^2}{a}\geq \frac{(\sum \frac{a}{b+c})^2}{a+b+c}=(\sum \frac{a}{b+c})^2\)
Tiếp tục áp dụng BĐT Cauchy-Schwarz:
\(\sum \frac{a}{b+c}=\sum \frac{a^2}{ab+ac}\geq \frac{(a+b+c)^2}{ab+ac+bc+ba+ca+cb}=\frac{(a+b+c)^2}{2(ab+bc+ac)}\\ =\frac{3(ab+bc+ac)}{2(ab+bc+ac)}=\frac{3}{2}\)
$\Rightarrow \sum \frac{a}{(1-a)^2}\geq (\frac{3}{2})^2=\frac{9}{4}$
Đúng 1
Bình luận (0)
