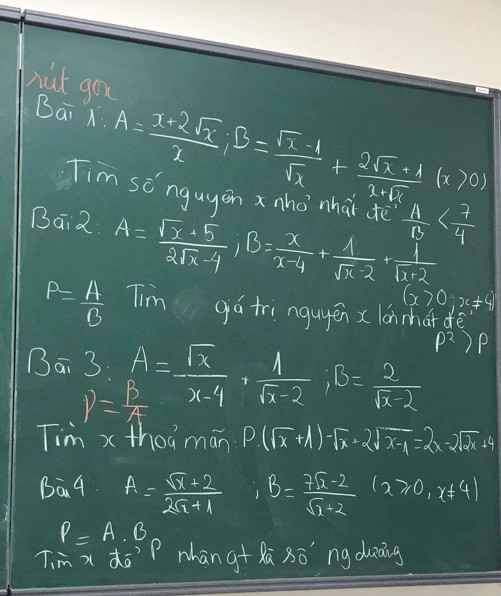Bài 4:
ĐKXĐ: x>=0
P=A*B
\(=\dfrac{\sqrt{x}+2}{2\sqrt{x}+1}\cdot\dfrac{7\sqrt{x}-2}{\sqrt{x}+2}\)
\(=\dfrac{7\sqrt{x}-2}{2\sqrt{x}+1}\)
Để P là số nguyên dương thì \(\left\{{}\begin{matrix}7\sqrt{x}-2⋮2\sqrt{x}+1\\P>0\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}7\sqrt{x}-2>0\\14\sqrt{x}-4⋮2\sqrt{x}+1\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}\sqrt{x}>\dfrac{2}{7}\\14\sqrt{x}+7-11⋮2\sqrt{x}+1\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}x>\dfrac{4}{49}\\-11⋮2\sqrt{x}+1\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}2\sqrt{x}+1\in\left\{1;11\right\}\\x>\dfrac{4}{49}\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}2\sqrt{x}\in\left\{0;10\right\}\\x>\dfrac{4}{49}\end{matrix}\right.\Leftrightarrow x=25\left(nhận\right)\)
Thử lại, ta thấy x=25 thỏa mãn
Vậy: x=25
Bài 2:
ĐKXĐ: x>0 và x<>4
P=A:B
\(=\dfrac{\sqrt{x}+5}{2\left(\sqrt{x}-2\right)}:\left(\dfrac{x}{x-4}+\dfrac{1}{\sqrt{x}-2}+\dfrac{1}{\sqrt{x}+2}\right)\)
\(=\dfrac{\sqrt{x}+5}{2\left(\sqrt{x}-2\right)}:\left(\dfrac{x}{\left(\sqrt{x}-2\right)\left(\sqrt{x}+2\right)}+\dfrac{1}{\sqrt{x}-2}+\dfrac{1}{\sqrt{x}+2}\right)\)
\(=\dfrac{\sqrt{x}+5}{2\left(\sqrt{x}-2\right)}:\dfrac{x+\sqrt{x}+2+\sqrt{x}-2}{\left(\sqrt{x}+2\right)\left(\sqrt{x}-2\right)}\)
\(=\dfrac{\sqrt{x}+5}{2\left(\sqrt{x}-2\right)}\cdot\dfrac{\left(\sqrt{x}+2\right)\left(\sqrt{x}-2\right)}{x+2\sqrt{x}}\)
\(=\dfrac{\left(\sqrt{x}+5\right)}{2}\cdot\dfrac{\sqrt{x}+2}{\sqrt{x}\left(\sqrt{x}+2\right)}=\dfrac{\sqrt{x}+5}{2\sqrt{x}}\)
P^2>P
=>P(P-1)>0
=>\(\dfrac{\sqrt{x}+5}{2\sqrt{x}}\cdot\dfrac{\sqrt{x}+5-2\sqrt{x}}{2\sqrt{x}}>0\)
=>\(-\sqrt{x}+5>0\)
=>\(-\sqrt{x}>-5\)
=>\(\sqrt{x}< 5\)
=>0<=x<25
Kết hợp ĐKXĐ, ta được: \(\left\{{}\begin{matrix}0< x< 25\\x\ne4\end{matrix}\right.\)
=>Số nguyên x lớn nhất thỏa mãn là x=24