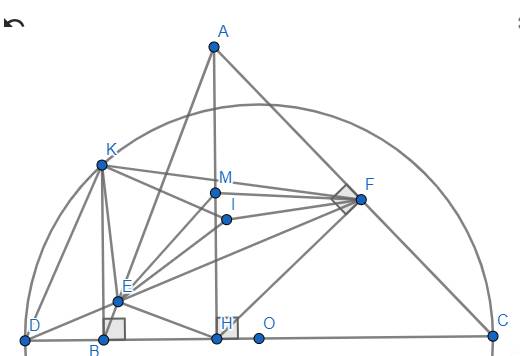
Nếu tính đến thời điểm hiện tại thì chắc chưa học tứ giác nội tiếp nên đây là lời giải KHÔNG theo cách tứ giác nội tiếp nhé (sau này học tứ giác nội tiếp rồi thì câu a, b sẽ giải ngắn hơn nhiều).
(a) Gọi \(M\) là trung điểm của \(AH\), suy ra \(MA=MH=\dfrac{AH}{2}\)
Các tam giác vuông \(AFH\), \(AEH\) lần lượt có \(FM\), \(EM\) là trung tuyến ứng với cạnh huyền \(AH\Rightarrow EM=FM=\dfrac{AH}{2}\).
Từ hai điều trên, suy ra \(A,E,H,F\) cùng nằm trên một đường tròn đường kính \(AH\) (đpcm).
(b) +) \(\Delta AHC\) vuông tại \(H\) có \(AF\cdot AC=AH^2\).
\(\Delta AHB\) vuông tại \(H\) có \(AE\cdot AB=AH^2\).
Từ đó, suy ra \(AF\cdot AC=AE\cdot AB\Leftrightarrow\dfrac{AE}{AC}=\dfrac{AF}{AB}\)
Xét \(\Delta AEF,\Delta ACB:\left\{{}\begin{matrix}\hat{A}\text{ chung}\\\dfrac{AE}{AC}=\dfrac{AF}{AB}\left(cmt\right)\end{matrix}\right.\)
\(\Rightarrow\Delta AEF\sim\Delta ACB\left(c.g.c\right)\Rightarrow\hat{AFE}=\hat{ABH}\).
Mà: \(\left\{{}\begin{matrix}\hat{ABH}+\hat{KBA}=\hat{KBH}=90^o\left(gt\right)\\\hat{AFE}+\hat{EFH}=\hat{AFH}=90^o\left(gt\right)\end{matrix}\right.\)
Vì vậy: \(\hat{KBA}=\hat{EFH}\left(đpcm\right)\)
+) Cũng từ \(\Delta AEF\sim\Delta ACB\) nên \(\hat{AEF}=\hat{C}\)
Lại có: \(\hat{AEF}=\hat{DEB}\) (đối đỉnh) nên \(\hat{DEB}=\hat{C}\).
Xét \(\Delta DEB,\Delta DCF\) có: \(\left\{{}\begin{matrix}\hat{D}\text{ chung}\\\hat{DEB}=\hat{C}\left(cmt\right)\end{matrix}\right.\)
\(\Rightarrow\Delta DEB\sim\Delta DCF\left(g.g\right)\)
\(\Rightarrow\dfrac{DE}{DC}=\dfrac{DB}{DF}\Rightarrow DE\cdot DF=DB\cdot DC\left(đpcm\right)\)
(c) (Câu này có dùng kiến thức góc tạo bởi tia tiếp tuyến và dây cung, không biết bạn đã học chưa:"D)
Xét \(\Delta DKC\) vuông tại \(K\) (\(\hat{K}=90^o\) do là góc nội tiếp chắn nửa đường tròn): \(DB\cdot DC=DK^2\)
Mà: \(DB\cdot DC=DE\cdot DF\left(cmt\right)\)
\(\Rightarrow DE\cdot DF=DK^2\Leftrightarrow\dfrac{DE}{DK}=\dfrac{DK}{DF}\).
Xét \(\Delta DEK,\Delta DKF:\) \(\left\{{}\begin{matrix}\hat{D}\text{ chung}\\\dfrac{DE}{DK}=\dfrac{DK}{DF}\left(cmt\right)\end{matrix}\right.\)
\(\Rightarrow\Delta DEK\sim\Delta DKF\left(g.g\right)\)
\(\Rightarrow\hat{DKE}=\hat{DFK}\).
Suy ra, \(DK\) là tiếp tuyến của đường tròn \(\left(I\right)\) hay \(IK\perp DK\) (đpcm).
Cho mình hỏi là bạn đã học tới tứ giác nội tiếp chưa nhỉ?