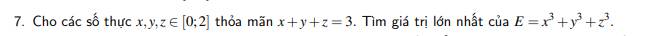Không mất tính tổng quát, giả sử \(x\) là số lớn nhất trong 3 số.
\(\Rightarrow1\le x\le2\) \(\Rightarrow\left(x-1\right)\left(x-2\right)\le0\)
Ta có:
\(E=x^3+y^3+z^3\le x^3+y^3+z^3+3yz\left(y+z\right)=x^3+\left(y+z\right)^3\)
\(\Rightarrow E\le x^3+\left(3-x\right)^3=9x^2-27x+27=9\left(x-1\right)\left(x-2\right)+9\le9\)
\(E_{max}=9\) khi \(\left(x;y;z\right)=\left(1;2;3\right)\) và các hoán vị