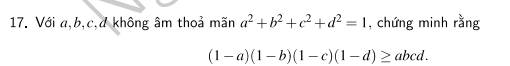Ta có:
\(\left(1-a\right)\left(1-c\right)=1+ac-a-c=\dfrac{1}{2}\left(a^2+b^2+c^2+d^2\right)+\dfrac{1}{2}+ac-a-c\)
\(=\dfrac{1}{2}\left(b^2+d^2\right)+\dfrac{1}{2}\left(2a^2+2c^2+2ac-2a-2c+1\right)\)
\(=\dfrac{1}{2}\left(b^2+d^2\right)+\dfrac{1}{2}\left(a+c-1\right)^2\)
\(\Rightarrow\left(1-a\right)\left(1-c\right)\ge\dfrac{1}{2}\left(b^2+d^2\right)\) (1)
Tương tự ta có: \(\left(1-b\right)\left(1-d\right)\ge\dfrac{1}{2}\left(a^2+c^2\right)\) (2)
Do \(a^2+b^2+c^2+d^2=1\Rightarrow\) a;b;c;d \(\in\left[0;1\right]\) \(\Rightarrow\) các vế của (1) và (2) đều không âm, nhân vế với vế:
\(\left(1-a\right)\left(1-b\right)\left(1-c\right)\left(1-d\right)\ge\dfrac{1}{4}\left(a^2+c^2\right)\left(b^2+d^2\right)\ge abcd\) (đpcm)