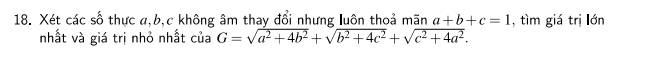Ta có:
\(\left(a^2+4b^2\right)\left(1+4\right)\ge\left(a+4b\right)^2\Rightarrow\sqrt{a^2+4b^2}\ge\dfrac{1}{\sqrt{5}}\left(a+4b\right)\)
Tương tự và cộng lại:
\(G\ge\dfrac{1}{\sqrt{5}}\left(5a+5b+5c\right)=\sqrt{5}\)
\(G_{min}=\sqrt{5}\) khi \(a=b=c=\dfrac{1}{3}\)
Lại có:
\(G=\sqrt{a^2+4b^2}+\sqrt{b^2+4c^2}+\sqrt{c^2+4a^2}\)
\(G\le\sqrt{a^2+4b^2+4ab}+\sqrt{b^2+4c^2+4bc}+\sqrt{c^2+4a^2+4ca}\)
\(G\le a+2b+b+2c+c+2a=3\)
\(G_{max}=3\) khi \(\left(a;b;c\right)=\left(0;0;1\right)\) và hoán vị
Đúng 1
Bình luận (0)
