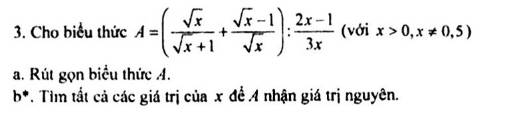Lời giải:
a.
\(A=\frac{\sqrt{x}.\sqrt{x}+(\sqrt{x}-1)(\sqrt{x}+1)}{\sqrt{x}(\sqrt{x}+1)}.\frac{3x}{2x-1}=\frac{2x-1}{\sqrt{x}(\sqrt{x}+1)}.\frac{3x}{2x-1}\\ =\frac{3x}{\sqrt{x}(\sqrt{x}+1)}=\frac{3\sqrt{x}}{\sqrt{x}+1}\)
b.
\(A=\frac{3\sqrt{x}}{\sqrt{x}+1}=\frac{3(\sqrt{x}+1)-3}{\sqrt{x}+1}=3-\frac{3}{\sqrt{x}+1}\)
Để $A$ nguyên thì $\frac{3}{\sqrt{x}+1}$ nguyên
Đặt $\frac{3}{\sqrt{x}+1}=t(t\in\mathbb{Z}$)
$\Rightarrow \sqrt{x}+1=\frac{3}{t}$
$\sqrt{x}=\frac{3-t}{t}$
Do $x>0$ nên $\frac{3-t}{t}>0\Leftrightarrow 0< t< 3$
Vì $t$ nguyên nên $t=1$ hoặc $t=2$
Nếu $t=1$ thì: $\sqrt{x}=2$ hay $x=4$ (tm)
Nếu $t=2$ thì $\sqrt{x}=\frac{1}{2}\Rightarrow x=\frac{1}{4}$ (tm)