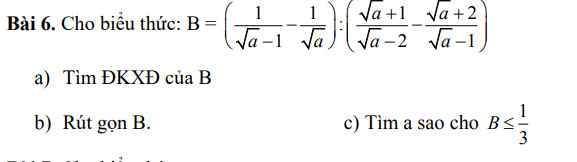Lời giải:
a. ĐKXĐ: $a>0; a\neq 1; a\neq 4$
b.
\(B=\frac{\sqrt{a}-(\sqrt{a}-1)}{\sqrt{a}(\sqrt{a}-1)}: \frac{(\sqrt{a}+1)(\sqrt{a}-1)-(\sqrt{a}+2)(\sqrt{a}-2)}{(\sqrt{a}-2)(\sqrt{a}-1)}\)
\(=\frac{1}{\sqrt{a}(\sqrt{a}-1)}:\frac{a-1-(a-4)}{(\sqrt{a}-2)(\sqrt{a}-1)}=\frac{1}{\sqrt{a}(\sqrt{a}-1)}:\frac{3}{(\sqrt{a}-2)(\sqrt{a}-1)}\\ =\frac{1}{\sqrt{a}(\sqrt{a}-1)}.\frac{(\sqrt{a}-2)(\sqrt{a}-1)}{3}\\ =\frac{\sqrt{a}-2}{3\sqrt{a}}\)
c.
\(B\leq \frac{1}{3}\Leftrightarrow \frac{\sqrt{a}-2}{3\sqrt{a}}-\frac{1}{3}\leq 0\\ \Leftrightarrow \frac{\sqrt{a}-2-\sqrt{a}}{3\sqrt{a}}\leq 0\\ \Leftrightarrow \frac{-2}{3\sqrt{a}}\leq 0\\\) (luôn đúng với mọi $a\in ĐKXĐ$)
Vâ $a>0; a\neq 1; a\neq 4$ thì $B\leq \frac{1}{3}$