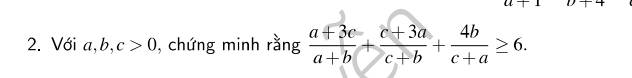Chuẩn hoá \(a+b+c=1\)
Ta có:
\(VT=a\left(\dfrac{1}{a+b}+\dfrac{3}{c+b}\right)+c\left(\dfrac{3}{a+b}+\dfrac{1}{c+b}\right)+\dfrac{4b}{c+a}\)
\(\ge a.\dfrac{16}{a+b+3\left(c+b\right)}+c.\dfrac{16}{3\left(a+b\right)+c+b}+\dfrac{4b}{c+a}\)
\(=8\left(\dfrac{2a}{a+4b+3c}+\dfrac{2c}{3a+4b+c}\right)+\dfrac{4b}{c+a}\)
\(=8\left(\dfrac{2a}{a+4b+3c}+1+\dfrac{2c}{3a+4b+c}+1\right)+\dfrac{4b}{c+a}-8.2\)
\(=8\left(3a+4b+3c\right)\left(\dfrac{1}{a+4b+3c}+\dfrac{1}{3a+4b+c}\right)+\dfrac{4b}{c+a}-8.2\)
\(\ge8\left(3a+4b+3c\right).\dfrac{1}{a+2b+c}+\dfrac{4b}{c+a}-8.2\)
\(=8\left(3+b\right)\dfrac{1}{1+b}+\dfrac{4b}{1-b}-8.2\)
\(=4\left[\dfrac{2\left(3+b\right)}{1+b}+\dfrac{b}{1-b}\right]-8.2\)
Ta có \(\dfrac{2\left(3+b\right)}{1+b}+\dfrac{b}{1-b}\ge\dfrac{11}{2}\left(\text{*}\right)\) với \(0< b< 1\)
Thật vậy \(\left(\text{*}\right)\Leftrightarrow4\left(3+b\right)\left(1-b\right)+2b\left(1+b\right)\ge11\left(1-b\right)\left(1+b\right)\)
\(\Leftrightarrow9b^2-6b+1\ge0\Leftrightarrow\left(3b-1\right)^2\ge0\), đúng
\(\Rightarrow VT\ge\dfrac{4.11}{2}-8.2=6\)
Đẳng thức xảy ra khi \(a=b=c=\dfrac{1}{3}\)