Bài 14:
a: Thay x=0 và y=3 vào hàm số \(y=\left(m-2\right)x+2m-5\),ta được:
\(0\cdot\left(m-2\right)+2m-5=3\)
=>2m-5=3
=>2m=8
=>m=4
b: Khi m=4 thì \(y=\left(4-2\right)x+2\cdot4-5=2x+3\)
Lập bảng giá trị:
| x | 0 | 1 |
| y=2x+3 | 3 | 5 |
Vẽ đồ thị:
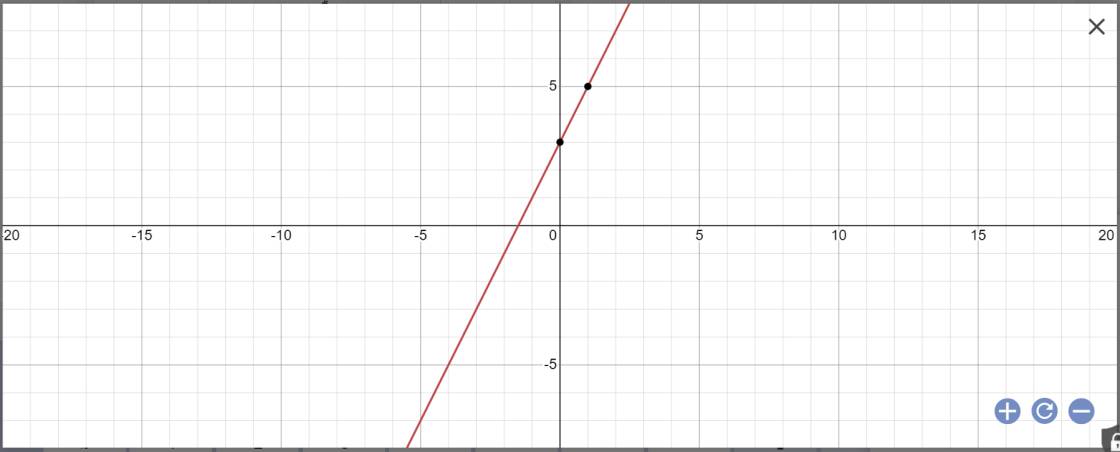
c: (d1): 2x-y+3=0
=>y=2x+3
Để (d) vuông góc với (d1) thì \(2\cdot\left(m-2\right)=-1\)
=>2m-4=-1
=>2m=3
=>\(m=\dfrac{3}{2}\)
d: (d): y=(m-2)x+2m-5
=mx-2x+2m-5
=m(x+2)-2x-5
Tọa độ điểm mà (d) luôn đi qua là:
\(\left\{{}\begin{matrix}x+2=0\\y=-2x-5\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}x=-2\\y=-2\cdot\left(-2\right)-5=4-5=-1\end{matrix}\right.\)
e: Khoảng cách từ M(2;0) đến (d): (m-2)x-y+2m-5=0 là:
\(d\left(M;\left(d\right)\right)=\dfrac{\left|2\cdot\left(m-2\right)+0\cdot\left(-1\right)+2m-5\right|}{\sqrt{\left(m-2\right)^2+1}}\)
\(=\dfrac{\left|2m-4+2m-5\right|}{\sqrt{\left(m-2\right)^2+1}}=\dfrac{\left|4m-9\right|}{\sqrt{\left(m-2\right)^2+1}}\)
Để d(M;(d)) lớn nhất thì 4m-9=0
=>4m=9
=>\(m=\dfrac{9}{4}\)
Bài 13:
a: Để hàm số (1) đồng biến trên R thì m-1>0
=>m>1
b: Để (1) có hệ số góc là 2 thì m-1=2
=>m=2+1
=>m=3
c: Thay x=2 và y=-1 vào (1), ta được:
\(2\left(m-1\right)+2=-1\)
=>2m-2+2=-1
=>2m=-1
=>\(m=-\dfrac{1}{2}\)
d:
(1): y=(m-1)x+2
Gọi A(x,y) và B(x,y) lần lượt là tọa độ giao điểm của (1) với hai trục Ox và Oy
Tọa độ A là:
\(\left\{{}\begin{matrix}y=0\\\left(m-1\right)x+2=0\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}y=0\\x\left(m-1\right)=-2\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}y=0\\x=\dfrac{-2}{m-1}\end{matrix}\right.\)
=>\(A\left(-\dfrac{2}{m-1};0\right)\)
\(OA=\sqrt{\left(-\dfrac{2}{m-1}-0\right)^2+\left(0-0\right)^2}=\sqrt{\left(-\dfrac{2}{m-1}\right)^2}=\dfrac{2}{\left|m-1\right|}\)
Tọa độ B là:
\(\left\{{}\begin{matrix}x=0\\y=\left(m-1\right)\cdot x+2=0\cdot\left(m-1\right)+2=2\end{matrix}\right.\)
=>B(0;2)
\(OB=\sqrt{\left(0-0\right)^2+\left(2-0\right)^2}=\sqrt{2^2}=2\)
Vì Ox\(\perp\)Oy
nên OA\(\perp\)OB tại O
=>\(S_{AOB}=\dfrac{1}{2}\cdot OA\cdot OB=\dfrac{1}{2}\cdot2\cdot\dfrac{2}{\left|m-1\right|}=\dfrac{2}{\left|m-1\right|}\)
Để \(S_{AOB}=4\) thì \(\dfrac{2}{\left|m-1\right|}=4\)
=>\(\left|m-1\right|=\dfrac{2}{4}=\dfrac{1}{2}\)
=>\(\left[{}\begin{matrix}m-1=\dfrac{1}{2}\\m-1=-\dfrac{1}{2}\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}m=\dfrac{3}{2}\\m=\dfrac{1}{2}\end{matrix}\right.\)















